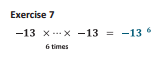Why mathematics curriculum reform is always so challenging

Because everyone wants to cram something else in.

Factoring tricks

As previously mentioned, I've been working with a non-profit that runs after school tutoring programs helping with the math side. Part of the problem is that the program leans toward the humanities side and some of the tutors are not at all comfortable with math.

I've been throwing together some short, smart-phone friendly videos for this target audience.




Everything here is modular. I dictated the scripts to dragon, created SVG graphics in Inkscape, put together the slide in Impress and PowerPoint, recorded the audio in Audacity and did the final edit in KDENlive. It's quick, not slick, but it is set up in a way that any given element can easily be changed.

Any feedback is appreciated.

Math for Tutors

I'm scheduled to give a math teaching seminar next month for a local nonprofit that tutors kids in urban neighborhoods. The primary focus of the program is language arts but inevitably, kids need help with their math homework.

The tutors are all volunteers and in terms of mathematical ability and comfort level, they range from artists to rocket scientists (and keep in mind, in Los Angeles, the term "rocket scientist" is not a euphemism).

Fractions and decimals are a frequent area of difficulty for many of the volunteers, so I was asked to put together an introduction and some basic teaching tips on the topic. I was also asked to address another area of great frustration for the tutors, Common Core.

How can you come up with a productive two-hour presentation on mathematical pedagogy with an audience that ranges from BFA's in drama to PhD's in engineering?



My partial solution was to come up with some quick, short, simple videos on basic topics like prime factors and using scientific calculators. You can see the first two on the blog's YouTube channel. They aren't pretty and the sound quality is somewhat embarrassing in places, but I'm hoping that they might provide enough of the background for me to jump directly into doing examples without having to spend significant amounts of time explaining the basics.

If you're curious, take a look. Any and all feedback is appreciated.

Tic-Tac-Toe (with Xs only)

I'll need to dig into this series a bit further when I get a chance.

Perfecting the imperfect [repost]

[disclaimer -- I've only field tested the first of these, so I can't guarantee that all of the variations will play smoothly. On the bright side, there ought to be plenty of room for improvement. As with all discussions of game variants, you should probably assume that countless people have already come up with any idea presented here.]

When the subject of perfect information games comes up, you probably think of chess, checkers, go, possibly Othello/Reversi and, if you're really into board games, something obscure like Agon. When you think of games of imperfect information, the first things that come to mind are probably probably card games like poker or a board game with dice-determined moves like backgammon and, if you're of a nostalgic bent, dominoes.

We can always make a perfect game imperfect by adding a random element or some other form of hidden information. In the chess variant Kriegspiel, you don't know where your opponent's pieces are until you bump into them. The game was originally played with three boards and a referee but the advent of personal computing has greatly simplified the process.

For a less elaborate version of imperfect chess, try adding a die-roll condition to certain moves. For example, if you attempt to capture and roll a four or better, the capture is allowed, if you roll a two or a three, you return the pieces to were they were before the capture (in essence losing a turn) and if you roll a one, you lose the attacking piece. Even a fairly simple variant such as this can raise interesting strategic questions.

But what about going the other way? Can we modify the rules of familiar games of chance so that they become games of perfect information? As far as I can tell the answer is yes, usually by making them games of resource allocation.

I first tried playing around with perfecting games because I'd started playing dominoes with a bluesman friend of mine (which is a bit like playing cards with a man named Doc). In an attempt to level the odds, I suggested playing the game with all the dominoes face up. We would take turns picking the dominoes we wanted until all were selected then would play the game using the regular rules. (We didn't bother with scoring -- whoever went out first won -- but if you want a more traditional system of scoring, you'd probably want to base it on the number of dominoes left in the loser's hand)

I learned two things from this experiment: first, a bluesman can beat you at dominoes no matter how you jigger the rules; and second, dominoes with perfect information plays a great deal like the standard version.

Sadly dominoes is not played as widely as it once was but you can try something similar with dice games like backgammon. Here's one version.

Print the following repeatedly on a sheet of paper:

Each player gets as many sheets as needed. When it's your turn you choose a number, cross it out of the inverted pyramid then move your piece that many spaces. Once you've crossed out a number you can't use it again until you've crossed out all of the other numbers in the pyramid. Obviously this means you'll want to avoid situations like having a large number of pieces two or three spaces from home.

If and when you cross off all of the numbers in one pyramid you start on the next. There's no limit to the number of pyramids you can go through. Other than that the rules are basically the same as those of regular backgammon except for a couple of modifications:

You can't land on the penultimate triangle (you'd need a one to get home and there are no ones in this variant);

If all your possible moves are blocked, you get to cross off two numbers instead of one (this discourages overly defensive play).

I haven't had a chance to field test this one, but it should be playable and serve as at least a starting point (let me know if you come up with something better). The same inverted pyramid sheet should be suitable for other dice based board games like parcheesi and maybe even Monopoly (though I'd have to give that one some thought).

I had meant to close with a perfected variant of poker but working out the rules is taking a bit longer than I expected. Maybe next week.

In the meantime, any ideas, improvement, additions?

Originally posted in West Coast Stat Views

Hexagonal Reversi

[If you don't have a hexboard lying around the house, you might consider going by the Amazon store for the board game Kruzno.]

Hexagonal Reversi is very similar to regular Reversi (which is suspiciously similar to Othello, but that's a subject for another post).

Here are the starting positions:

Each player takes turns placing one of his or her pieces on the board so that at least one row of the opponent's pieces lie between the newly placed piece and another piece already on the board at which point the row of opponent's pieces are replaced with the player's pieces.

This figure above shows the possible initial moves if black goes first (B) or if white goes first (W).


[repostedd from 2014]

MOOCs -- this time it's different

Timothy Taylor highlights an interesting passage from this paper by Michael S. McPherson and Lawrence S. Bacow.

     "Berland (1992), citing a popular commentator named Waldeman Kaempffert writing in 1924, reported that “there were visions of radio producing ‘a super radio orchestra’ and ‘a super radio university’ wherein ‘every home has the potentiality of becoming an extension of Carnegie Hall or Harvard University.’” Craig (2000) reports that “the enthusiasm for radio education during the early days of broadcasting was palpable. Many universities set up broadcast stations as part of their extension programs and in order to provide their engineering and journalism students with experience in radio. By 1925 there were 128 educational stations across the country, mostly run by tertiary institutions” (p. 2831). The enthusiasm didn’t last—by 1931 the number of educational stations was down to 49, most low-powered (p. 2839). This was in part the result of cumbersome regulation, perhaps induced by commercial interests; but the student self-control problem ... likely played a role as well. As NBC representative Janice Waller observed, “Even those listeners who clamored for educational programs, Waller found, secretly preferred to listen to comedians such as Jack Benny. These “intellectually dishonest” people “want to appear very highbrow before for their friends . . . but down inside, and within the confines of their own homes, they are, frankly, bored if forced to listen to the majority of educational programs” (as quoted in Craig 2000, pp. 2865–66).

    "The excitement in the late 1950s about educational television outshone even the earlier enthusiasm for radio. An article by Schwarzwalder (1959, pp. 181–182) has an eerily familiar ring: “Educational Television can extend teaching to thousands, hundreds of thousands and, potentially, even millions. . . . As Professor Siepman wrote some weeks ago in The New York Times, ‘with impressive regularity the results come in. Those taught by television seem to do at least as well as those taught in the conventional way.’ . . . The implications of these facts to a beleaguered democracy desperately in need of more education for more of its people are immense. We shall ignore these implications at our national peril.” Schwartzman goes on to claim that any subject, including physics, manual skills, and the arts can be taught by television, and even cites experiments that show “that the discussion technique can be adapted to television.”"

Rutgers vs. DeVry

Dean Dad has some interesting (and, based on my experience, valid) observations on teaching at both ends of the prestige spectrum.

Prestigious places tend to be selective, which is to say, they tend only to let in students who have shown the ability to be very successful in traditional high school settings.  These are the students who take lots of Honors classes, run clubs, volunteer, and get high grades.  Students like that are good at school; if they weren’t, they wouldn’t get in.  That frees up faculty to spend relatively little time worrying about pedagogy; they can just present the material and trust that most of the students will get it.  At Rutgers, for example, many undergraduate classes were so large that there wasn’t much choice but to lecture.  Lectures can be “cognitively complex” at a very high level.

When I taught at DeVry, though, I had to unlearn the teaching methods I had picked up at Rutgers, and pick up a whole new set.  These students generally weren’t good at school, or if they were, they didn’t know it.  They didn’t need to have certainties deconstructed; they needed to feel like there was a point in even trying.  I learned quickly, and the hard way, the difference between “what I say” and “what they hear.”  I had to shift focus.  Instead of showing unexpected nuance and depth to a seemingly simple issue (in the ‘90’s, we called that “problematizing”), I had to bring clarity to what was otherwise a frustrating fog.  That’s a different task, requiring different methods.  Lecture had to be cut into small pieces, interspersed among as many applications as possible. 

After a couple of years of teaching at DeVry, I was a far better teacher than I had ever been at Rutgers.  At a basic level, it mattered more.  The top students there -- and there were some -- got some pretty terrific classes, if I do say so myself, and I wasn’t the best teacher there. 

At research universities, faculty are hired and promoted based on research.  I had professors in grad school tell me openly and without shame to minimize the amount of time I spent on teaching, in order to spend more time writing.  In a culture like that, I’m not shocked to discover that much of the teaching is done by lecture. 

Where the “prestige” piece is more relevant is outside of class.  That’s where the ‘signaling’ piece of a selective degree comes into play.  But inside class, I’m not shocked to hear that the gap is small, when it exists at all.  And given the academic job market of the last twenty years, teaching-intensive places have been able to hire from the same pool that the elites have; by now, you can get “cognitively complex” faculty at every level. 

The Blue and the Gray

[Reprinted from 2012]

The famous game designer,* Sid Sackson, had over eighteen thousand games in his personal collection so making his short list was quite an accomplishment, particularly for a game that almost nobody has ever heard of.

On this alone, the Blue and the Gray would be worth a look, but the game also has a number of other points to recommend it: it only takes about three minutes to learn (you can find a complete set of rules here); it is, as far as I know, unique; it raises a number of interesting and unusual strategic questions; and for the educators out there, its Turn-of-the-Century** origins provide some opportunities for teaching across the curriculum. My only major complaint is that it requires a dedicated board, but making your own shouldn't take more than a few minutes.

The object of the game is to be the first to get your general to the center by moving along the designated path while using your soldiers to block your opponent's progress. Since soldiers can capture each other, the game has two offensive options (capturing and advancing) compared to one defensive option (blocking). (Something I learned from developing my own game was the more the designer can shift the focus to offense, the better and faster the game will play.)

I don't know of any attempt to do a serious analysis of the Blue and the Gray. Might be fun to look into. If someone out there finds anything interesting, make sure to let us know.


* Yes, I did just use the phrase, 'famous game designer.'

** I'm going off memory here about the age of the game. You should probably double check before building a lesson plan around this. (see update)

From West Coast Stat Views

UPDATE:

Via the good people at the University of Maryland, here's the original patent from 1903.

Facade Chess [reprint]

[disclaimer -- there are no new chess variants. I don't know who came up with this idea first but I'm pretty sure it wasn't me.]

By most reasonable standards, there are too many chess variants out there already. A few are actually worth playing (such Gliński's hexagonal game), the rest are of interest, if it all, more as thought experiments and programming problems.

One potentially promising area for the latter is variants of imperfect information, which leads us to familiar games like kriegspiel and this variant, facade chess.

Start with a standard board and pieces. When I say standard pieces I mean that you will have one piece that moves like a king, one piece that moves like a queen, two pieces that move like bishops and so on.

The pieces' appearance, however, will not be standard. They will look like tiny replicas of those A-frame signs restaurants put out on the sidewalk, with slots for pictures of chess pieces on either side. On most of the pieces, the picture is the same on the front and the back, but on up to three (or some other agreed on number), the pictures have been switched.

Pieces are lined up in standard position based the picture in the front but they have to move in accordance with the picture on the back (like kriegspiel, this game definitely needs a referee). If for example, the queen had a rook's picture on front of it, you would put it in a corner but you could move it any distance vertically, horizontally or diagonally.

Each move has to be weighed in terms of both position achieved and information revealed -- as soon as that rook moves diagonally, the other player will know something's up. In addition to deduction you can also find out the true identity of a piece by capturing it. Capturing a disguised piece also provides useful information about the disguised pieces still on the board.

I'm not sure how playable facade chess would be -- players would probably tend to under utilize their pieces (moving rooks like pawns or queens like bishops so as not to give away their identities) -- making for a slow game but from an analytic standpoint, the variant could still provide interesting problems. Chess strategies are complex to start with; imagine adding a layer of uncertainty and questions about how much value to put on concealing information.

The Humble Checker

Yet to calculate is not in itself to analyze. A chess-player, for example, does the one without effort at the other. It follows that the game of chess, in its effects upon mental character, is greatly misunderstood. I am not now writing a treatise, but simply prefacing a somewhat peculiar narrative by observations very much at random; I will, therefore, take occasion to assert that the higher powers of the reflective intellect are more decidedly and more usefully tasked by the unostentatious game of draughts than by all the elaborate frivolity of chess. In this latter, where the pieces have different and bizarre motions, with various and variable values, what is only complex is mistaken (a not unusual error) for what is profound. The attention is here called powerfully into play. If it flag for an instant, an oversight is committed, resulting in injury or defeat. The possible moves being not only manifold but involute, the chances of such oversights are multiplied; and in nine cases out of ten it is the more concentrative rather than the more acute player who conquers. In draughts, on the contrary, where the moves are unique and have but little variation, the probabilities of inadvertence are diminished, and the mere attention being left comparatively what advantages are obtained by either party are obtained by superior acumen.

Edgar Allan Poe -- "The Murders in the Rue Morgue"

Poe's opinion on this matter is more common than you might expect. It's not unusual to hear masters of both chess and checkers (draughts) to admit that they prefer the latter. So why does chess get all the respect? Why do you never see a criminal mastermind or a Bond villain playing in a checkers tournament?

Part of the problem is that we learn the game as children so we tend to think of it as a children's game. We focus on how simple the rules are and miss how much complexity and subtlety you can get out of those rules.

Chess derives most of its complexity through differentiated pieces; with checkers the complexity comes from the interaction between pieces. The result is a series of elegant graph problems where the viable paths change with each move of your opponent. To draw an analogy with chess, imagine if moving your knight could allow your opponent's bishop to move like a rook. Add to that the potential for traps and manipulation that come with forced capture and you have one of the most remarkable games of all time.

There have been any number of checkers variants.* You could even argue that all checkers games are variants since, unlike chess, there is no single, internationally recognized version. Here are some of the best and best-known.



Spanish Checkers

Considered by many connoisseurs to be the best of the national variants. It is distinguished from the American version by a queen's (analogous to a king) ability to jump long. This makes a queen powerful but, since captures are mandatory, easier to capture.






Dama (Turkish Checkers)

Also known as Greek checkers. In this variant, pieces move vertically and horizontally instead of diagonally. Among other things this doubles the playing field.



Lasca

This variant was invented by the second World Chess Champion Emanuel Lasker. It's worth noting that Lasker (who is considered one of the best chess players of all time) would look to checkers when designing his own game.

In Lasca, captured pieces are added to the bottom of columns controlled by whichever player has the top piece. Since jumping only captures the piece on top of the column, players have to take into account not only position but also height and position.

You can get a detailed write-up by following the link or you can see Lasker's original patent application here. He comes off as rather immodest, but he was the world's best chess player and a close friend of Einstein so I guess we can let him slide.


Misère checkers

This one you probably know as suicide or give-away checkers. The object is either to lose all your pieces or have them blocked so that you can't move.



Endless Checkers (or whatever the damned thing is called)

I'm certain I've read about this somewhere though I can't seem to find any record of it. Here, when a piece reaches the last it can move to an appropriate space on the first row (think of a board wrapped around a cylinder). There are no kings in endless checkers.


I have a feeling I'm missing something. Any suggestions?

* Including one I'm particularly fond of, but that's a topic for another post.

[This is a repost.]

Kriegspiel and Dark Chess

[I'm going to be doing a math games retrospective for the next few weeks mixing new posts with reprints of some old favorites. The following first appeared in 2013.]

I've been talking about games of perfect information and I have another post on the subject coming up so this seems like a good time to mention two of the best known chess variants of imperfect information.

From the nice people at Wikipedia:

Kriegspiel (German for war game) is a chess variant invented by Henry Michael Temple in 1899 and based upon the original Kriegsspiel developed by Georg von Rassewitz in 1812.[1][2] In this game each player can see their own pieces, but not those of their opponent. For this reason, it is necessary to have a third person (or computer) act as a referee, with full information about the progress of the game. When it is a player's turn he will attempt a move, which the referee will declare to be 'legal' or 'illegal'. If the move is illegal, the player tries again; if it is legal, that move stands. Each player is given information about checks and captures. They may also ask the referee if there are any legal captures with a pawn.

and

Dark chess is a chess variant with incomplete information, similar to Kriegspiel. It was invented by Jens Bæk Nielsen and Torben Osted in 1989. A player does not see the entire board, only their own pieces (including pawns), and squares where these pieces could move.

I've never actually played either of these games (I have enough trouble with unvaried chess), but they raise all sorts of interesting questions about forming a strategy with incomplete information.

Risky Business -- board game math lessons

[I'm going to be doing a math games retrospective for the next few weeks mixing new posts with reprints of some old favorites. The following first appeared in 2012.]




"Let's play Twister; let's play Risk."

No, seriously, let's play Risk, or at least talk about playing Risk. In case you're not familiar with the game, here's the Wikipedia summary

Risk is a turn-based game for two to six players. The standard version is played on a board depicting a political map of the Earth, divided into forty-two territories, which are grouped into six continents. The primary object of the game is "world domination," or "to occupy every territory on the board and in so doing, eliminate all other players."[1] Players control armies with which they attempt to capture territories from other players, with results determined by dice rolls.

(invented by the director of the Red Balloon -- who knew?)

Risk can be a good taking off point for a number of lessons and assignments like:

1. Strategic thinking -- break the class into groups, have them write up rules and recommendations for the game then test these ideas in a tournament

2. (not math but why should that stop you?) -- what modern countries and provinces correspond to the regions on the board? What are they like? You might add naming these countries as a condition for conquering a region.

3. Probability -- what are the chances of taking a country with j attackers and k defenders? What's the expected strength of j if there is a conquest, k if the attack is repulsed?

But the main lesson I'd like to suggest is an introduction to graphs. We have other graph based games and puzzles in our tool chest such as doublets and the six degrees game but Risk is probably the most familiar to the kids. More importantly, it requires actually working with graphs as part of a larger problem.

After the students are acquainted with the game, explain the basic terms of graph theory then show them something like this subgraph of North America

Ask the students to do the following (After checking to make sure I got this right) :

1. Fill in the other countries

2. Explain what's special about nodes like Alaska and Greenland

3. Draw subgraphs of each continent

4. Find the shortest path between various pairs of countries
  4b Find the shortest path between various pairs of countries when certain territories (particularly Russia) are blocked
  4c (advanced) With randomly placed armies, see which path would be easiest to conquer

5. Play a game on a node and edge board

6. Make up new node and edge boards. Give the territories real or mythical names. Try playing a few games on them.

Pedagogy lessons from Office Space -- don't give open-ended instructions if you will only accept a specific response

Early in my corporate career I worked for a very Dilbert-esque where the managers had an annoying way of buzzing around what they actually meant to say. Even when you figured out what they were getting at, they refused to be pinned down.

Many of those conversations sounded remarkably like this:



37 Pieces of Flair from Lloyd Wilson on Vimeo.


This has always been a problem in teaching. Open-ended questions and instructions are highly useful, even necessary when trying to get students to be more independent and develop problem-solving skills, but the flipside is you have to be prepared for a response other than the one you had in mind.You also have to listen closely and decide whether a response was right, wrong or somewhere in between. Open-ended questions are best used as part of a conversation; they can be highly problematic as part of a written assignment.

The problem has gotten much worse with the rise of the education reform movement. As mentioned before, the movement has a history of picking up techniques but leaving behind essential context. The result has been a steady stream of students given vague questions then penalized for having the "wrong" correct answer.

Colbert brings us "Nerds vs. Robots"

Monday Video: Robot Cheetah -- Now Even Cooler

From the good people at MIT:

Now, the robot can “see,” with the use of onboard LIDAR — a visual system that uses reflections from a laser to map terrain. The team developed a three-part algorithm to plan out the robot’s path, based on LIDAR data. Both the vision and path-planning system are onboard the robot, giving it complete autonomous control.

The algorithm’s first component enables the robot to detect an obstacle and estimate its size and distance. The researchers devised a formula to simplify a visual scene, representing the ground as a straight line, and any obstacles as deviations from that line. With this formula, the robot can estimate an obstacle’s height and distance from itself.

Once the robot has detected an obstacle, the second component of the algorithm kicks in, allowing the robot to adjust its approach while nearing the obstacle. Based on the obstacle’s distance, the algorithm predicts the best position from which to jump in order to safely clear it, then backtracks from there to space out the robot’s remaining strides, speeding up or slowing down in order to reach the optimal jumping-off point.

We may differ on the definition of "has been corrected"

As part of a response the the recent piece in the Washington Post, Jill Diniz (Director of Eureka Math/Great Minds) said [emphasis added]:

The missing parentheses noted by the blogger, when introducing the concept of raising a negative number to a positive integer, was caused by converting the online curriculum to PDFs. This has been corrected. A benefit of open educational resources, such as Eureka Math, is they are easier than traditional instructional resources to improve upon quickly. 

Putting aside the concerns this raises about editing, proofing and overall quality control, let's take a minute and check the corrected version.

In case the print is too small, here are a couple of crops:

MOO?s

[I'm in full mad-scientist mode here, so things may be a bit incoherent in places but I do have some more realistic (or at least, less febrile) plans in the queue.]

MOOC advocates like Friedman have been both wildly ambitious about the potential impact of the technology and strangely timid about pushing its boundaries. Mostly, they fall back on the catalytic theory of educational technology. Rather than doing hard thinking about what different media are good at, they simply assume that the presence of technology will automatically make things better.

For all the talk about reinventing the form, MOOCS still tend to look pretty much like this:

A series of lessons and assignments given in a specific order, in other words, just like any other course..

Why are courses so linear? Because the current system is based on having instructors interact face-to-face with large numbers of students, and the only cost-efficient way to do this on a large scale is to collect the students in groups and take them through standardized instruction. We can go back-and-forth on the value of this face-to-face interaction, but it is clear that, once you have eliminated this requirement, you have no need for this level of standardization.

Even if we accept the necessity of having everybody take a common set of exams (and I am not entirely prepared to concede that one either), there is still no reason for all students in a MOOC to take the same instructional units in the same order.

Instead of thinking lesson one, lesson two, exam one, lesson three, exam two and so forth ad nauseam, we should probably be thinking more in the lines of this:

We have some kind of assessment. Based on the results of that assessment, the student is sent to a certain module. That module could be pretty much anything. The student could be directed to watch a video clip, listen to an audio file, read a section of text, play a game, chat with an instructor, or even have a tutoring session or study group. Even the assessments might vary based on path.

In addition to being customized to each student and allowing for an wide array of modules, the MOO? is an evolving format. Assessments can be changed, paths can shift, and, most importantly, more modules can always be added (possibly even user based content).

I know this is all very rough and inchoate, but I do plan to get specific in the near future, starting with our old friend, Eugen Weber.

From the ashes of New Math

One of my big concerns with the education reform debate, particularly as it regards mathematics, is that a great deal of the debate consist of words being thrown around that have a positive emotional connotation, but which are either vague or worse yet mean different things to different participants in the discussion.

As a result, you have a large number of "supporters" of common core who are, in fact, promoting entirely different agendas and probably not realizing it (you might be able to say the same about common core opponents but, by nature, opposition is better able to handle a lack of coherence) . I strongly suspect this is one of the causes behind the many problems we've seen in Eureka math and related programs. The various contributors were working from different and incompatible blueprints.

There's been a great deal of talk about improving mathematics education, raising standards, teaching problem-solving, and being more rigorous. All of this certainly sounds wonderful, but it is also undeniably vague. When you drill down, you learn that different supporters are using the same words in radically different senses .

For David Coleman and most of the non-content specialists, these words mean that all kids graduating high school should be college and career-ready, especially when it comes to the STEM fields which are seen as being essential to future economic growth.

(We should probably stop here and make a distinction between STEM and STEAM – science technology engineering applied mathematics. Coleman and Company are definitely talking about steam)

Professor Wu (and I suspect many of the other mathematicians who have joined into the initiative) is defining rigor much more rigorously. For him, the objective is to teach mathematics in a pure form, an axiomatic system where theorems build upon theorems using rules of formal logic. This is not the kind of math class that most engineers advocate; rather it is the kind of math class that most engineers complain about. (Professor Wu is definitely not a STEAM guy.)

In the following list taken from this essay from Professor Wu, you can get a feel for just how different his philosophy is from David Coleman's. The real tip-off is part 3. The suggestion that every formula or algorithm be logically derived before it can be used has huge implications, particularly as we move into more applied topics. (Who here remembers calculus? Okay, and who here remembers how to prove the fundamental theorem of calculus?)

All of Professor Wu's arguments are familiar to anyone who has studied the history of New Math in the 60s. There is no noticeable daylight between the two approaches.

I don't necessarily mean this as a pejorative. Lots of smart people thought that new math was a good idea in the late 50s and early 60s; I'm sure that quite a few smart people still think so today. I personally think it's a very bad idea but that's a topic for another post. For now though, the more immediate priority is just understand exactly what we're arguing about.

The Fundamental Principles of Mathematics

I believe there are five interrelated, fundamental principles of mathematics.
They are routinely violated in school textbooks and in the math education
literature, so teachers have to be aware of them to teach well.

1. Every concept is precisely defined, and definitions furnish the basis for logical
deductions. At the moment, the neglect of definitions in school mathematics has reached the point at which many teachers no longer know the difference between a definition and a theorem. The general perception among the hundreds of teachers I have worked with is that a definition is “one more thing to memorize.” Many bread-and-butter concepts of K–12 mathematics are not correctly defined or, if defined, are not put to use as integral parts of reasoning. These include number, rational number (in middle school), decimal (as a fraction in upper elementary school), ordering of fractions, product of fractions, division of fractions, length-area-volume (for different grade levels), slope of a line, half-plane of a line, equation, graph of an equation, inequality between functions, rational exponents of a positive number, polygon, congruence, similarity, parabola, inverse function, and polynomial.

2. Mathematical statements are precise. At any moment, it is clear what is known and what is not known. There are too many places in school mathematics in which textbooks and other education materials fudge the boundary between what is true and what is not. Often a heuristic argument is conflated with correct logical reasoning. For example, the identity √a√b = √ab for positive numbers a and b is often explained by assigning a few specific values to a and b and then checking for these values with a calculator. Such an approach is a poor substitute for mathematics because it leaves open the possibility that there are other values for a and b for which the identity is not true.

3. Every assertion can be backed by logical reasoning. Reasoning is the lifeblood of mathematics and the platform that launches problem solving. For example, the rules of place value are logical consequences of the way we choose to count. By choosing to use 10 symbols (i.e., 0 to 9), we are forced to use no more than one position (place) to be able to count to large numbers. Given the too frequent absence of reasoning in school mathematics, how can we ask students to solve problems if teachers have not been prepared to engage students in logical reasoning on a consistent basis?

4. Mathematics is coherent; it is a tapestry in which all the concepts and skills are logically interwoven to form a single piece. The professional development of math teachers usually emphasizes either procedures (in days of yore) or intuition (in modern times), but not the coherent structure of mathematics. This may be the one aspect of mathematics that most teachers (and, dare I say, also math education professors) find most elusive. For instance, the lack of awareness of the coherence of the number systems in K–12 (whole numbers, integers, fractions, rational numbers, real numbers, and complex numbers) may account for teaching fractions as “different from” whole numbers such that the learning of fractions becomes almost divorced from the learning of whole numbers. Likewise, the resistance that some math educators (and therefore teachers) have to explicitly teaching children the standard algorithms may arise from not knowing the coherent structure that underlies these algorithms: the essence of all four standard algorithms is the reduction of any whole number computation to the computation of single-digit numbers.

5. Mathematics is goal oriented, and every concept or skill has a purpose. Teachers who recognize the purposefulness of mathematics gain an extra tool to make their lessons more compelling. For example, when students see the technique of completing the square merely as a trick to get the quadratic formula, rather than as the central idea underlying the study of quadratic functions, their understanding of the technique is superficial. Mathematics is a collection of interconnecting chains in which each concept or skill appears as a link in a chain, so that each concept or skill serves the purpose of supporting another one down the line. Students should get to see for themselves that the mathematics curriculum moves forward with a purpose.

At the risk of putting too fine of a point on it, this approach tends to produce extremely formal and dense prose such the following (from a company Professor Wu was involved with):

Dilation: A transformation of the plane with center O and scale factor r(r > 0). If
D(O) = O and if P ≠ O, then the point D(P), to be denoted by Q, is the point on the ray OP so that |OQ| = r|OP|. If the scale factor r ≠ 1, then a dilation in the coordinate plane is a transformation that shrinks or magnifies a figure by multiplying each coordinate of the figure by the scale factor.

Congruence: A finite composition of basic rigid motions—reflections, rotations,
translations—of the plane. Two figures in a plane are congruent if there is a congruence that maps one figure onto the other figure.

Similar: Two figures in the plane are similar if a similarity transformation exists, taking one figure to the other.

Similarity Transformation: A similarity transformation, or similarity, is a composition of a finite number of basic rigid motions or dilations. The scale factor of a similarity transformation is the product of the scale factors of the dilations in the composition; if there are no dilations in the composition, the scale factor is defined to be 1.

Similarity: A similarity is an example of a transformation.

Opposite day at the Common Core debate

I recently came across this defense of Common Core by two Berkeley mathematicians, Edward Frenkel and Hung-Hsi Wu. Both are sharp and highly respected and when you hear about serious mathematicians supporting the initiative, there's a good chance these two names will be on the list that follows.

Except they don't support it. They support something they call Common Core, but what they describe is radically different than what the people behind the program are talking about. The disconnect is truly amazing. Wu and Frenkel's description of common core doesn't just disagree with that used by David Coleman and pretty much everyone else involved with the enterprise; it openly contradicts it.

The case that Coleman made to Bill Gates and stuck with since then is that "academic standards varied so wildly between states that high school diplomas had lost all meaning". Furthermore, Coleman argued that having a uniform set of national standards would allow us to use a powerful set of administrative tools. We could create metrics, track progress, set up incentive systems, and generally tackle the problem like management consultants.

Compare that to this excerpt from Wu and Frenkel's essay [emphasis added]:

Before the CCSSM were adopted, we already had a de facto national curriculum in math because the same collection of textbooks was (and still is) widely used across the country. The deficiencies of this de facto national curriculum of "Textbook School Mathematics" are staggering. The CCSSM were developed precisely to eliminate those deficiencies, but for CCSSM to come to life we must have new textbooks written in accordance with CCSSM. So far, this has not happened and, unfortunately, the system is set up in such a way that the private companies writing textbooks have more incentive to preserve the existing status quo maximizing their market share than to get their math right. The big elephant in the room is that as of today, less than a year before the CCSSM are to be fully implemented, we still have no viable textbooks to use for teaching mathematics according to CCSSM!

The situation is further aggravated by the rush to implement CCSSM in student assessment. A case in point is the recent fiasco in New York State, which does not yet have a solid program for teaching CCSSM, but decided to test students according to CCSSM anyway. The result: students failed miserably. One of the teachers wrote to us about her regrets that "the kids were not taught Common Core" and that it was "tragic" how low their scores were. How could it be otherwise? Why are we testing students on material they haven't been taught? Of course, it is much easier and more fun, in lieu of writing good CCSSM textbooks, to make up CCSSM tests and then pat each other on the back and wave a big banner: "We have implemented Common Core -- Mission accomplished." But no one benefits from this. Are we competing to create a Potemkin village, or do we actually care about the welfare of the next generation? What happened in New York State will happen next year across the country if we don't get our act together.

[As a side remark, we note that even in the best of circumstances, it's a big question how to effectively test students in math on a large scale. Developing such tests is an art form still waiting to be perfected, and in any case, it's not clear how accurately students' scores on these tests can reflect students' learning. Unfortunately, our national obsession with the test scores has forced teachers to teach to the test rather than teach the material for learning. While we consider some form of standardized assessment to be necessary (just as driver's license tests are necessary), we deplore this obsession. It is time to put the emphasis back on student learning inside the classroom.]

These misguided practices give a bad name to CCSSM, which is being exploited by the standards' opponents. They misinform the public by equating CCSSM with ill-fated assessments, such as the one in New York State, when in fact the problem is caused mostly by the disconnect between the current Textbook School Mathematics and CCSSM. It is for this reason that having the CCSSM is crucial, because this is what will ensure that students are taught correct mathematics rather than the deficient and obsolete Textbook School Mathematics.

It is possible and necessary to create mathematics textbooks that do better than Textbook School Mathematics. One such effort by commoncore.org holds promise: its Eureka Math series will make online courses in K-12 math available at a modest cost. The series will be completed sometime in 2014. [Full disclosure: one of us is an author of the 8th grade textbook in that series.]

The authors have contradicted both major components of Coleman's argument. They insist that we already have a relatively consistent national system of mathematics standards and furthermore they question the reliability of the metrics which Coleman's entire system is based upon.

How can proponents of common core hold such mutually exclusive use and yet be largely unaware of the contradictions?

I suspect it is some combination of poor communication and wishful thinking on both sides. As spelled out in this essay by Wu, the authors desperately want to see mathematics education returned to some kind of Euclidean ideal. A rigorous axiomatic approach where all lessons start with precise definitions and proceed through a series of logical deductions. They have convinced themselves that the rest of the Common Core establishment is in sympathy with them just as they have convinced themselves that the lessons being produced by Eureka math are rigorous and accurate.

Well, it's funny to math majors

A few years ago, when I was teaching math at a big state university, a colleague told me the following.

She was comparing notes with a professor at a nearby school on how their respective real analysis courses were going. She told him that they had just proved that the square root of two was an irrational number. He laughed and said she was way ahead of him; his class had just proved that the square root of two is a number.

[Don't feel bad if you don't get it. This is not the sort of thing that normal people talk about.]

The joke was that, while it may sound impressive, showing that the square root of two is irrational is fairly easy. There's a nice, elegant little proof that is easy to explain and is suitable for anyone who has completed the first few sections of high school algebra. On the other hand, showing that a real number X exist such that X squared equals two is actually a bit of a challenge.

There is one other point here which ties in to our ongoing math curriculum thread. Namely that, with the borderline exception of high school geometry (and even there we cheat a little), a truly rigorous approach to lower level mathematics is wildly impractical. The order in which concepts are needed does not match up at all with the order of difficulty of proof (the fundamental theorem of calculus comes to mind). Therefore much (probably most) of what we tell students is back up with no more than a "trust us." We don't have to like this but we do have to acknowledge it.

This doesn't mean that proofs aren't important, but that the importance lies in the process and not in the result.

Monday video -- summer break edition

Now that the students are gone we can let our hair down.

Eureka Math Tips for Parents -- worst SAT prep question ever

In the last installment (click here), I pointed to some extremely formal and difficult to read definitions such as this:

Similarity Transformation: A similarity transformation, or similarity, is a composition of a finite number of basic rigid motions or dilations. The scale factor of a similarity transformation is the product of the scale factors of the dilations in the composition; if there are no dilations in the composition, the scale factor is defined to be 1.

I argued that this level of rigor was inappropriate for eighth grade math, but that's only half the story. It is possible to make a case for teaching junior high kids using the language and structure of an abstract algebra class. Not a good case, in my opinion, but not a nonsensical one either.

If you can pull it off, there's something to be said for the axiomatic approach, having each statement emerge naturally from the postulates and theorems that came before. There is also something to be said for learning to formulate closely reasoned, exactly worded arguments. That's an experience probably best deferred until after puberty, but still...

What we have here, though, is something entirely different. The difficult technical language doesn't actually lead to anything. Students are dragged through these incredibly dense and confusing set-ups only to be have them followed by something like this (from the same lesson) [emphasis added]

No, even though we could say that the corresponding sides are in proportion, there exists no single rigid motion or sequence of rigid motions that would map a four-sided figure to a three-sided figure. Therefore, the figures do not fulfill the congruence part of the definition for similarity, and Figure A is not similar to Figure A′.

God, this is maddening. You can't say that "the corresponding sides are in proportion"; you can't say ANYTHING about the corresponding sides here. The term is meaningless when comparing a rectangle and a triangle.

From Wikipedia:

In geometry, the tests for congruence and similarity involve comparing corresponding sides of polygons. In these tests, each side in one polygon is paired with a side in the second polygon, taking care to preserve the order of adjacency. 

If you use this or any other kind of standard definition, that statement that has sides of a rectangle correspond to sides of a triangle is gibberish.

I suspect that the authors were trying to model their problem after something like this:

I didn't bother to label these but you get the idea. It is easy to come up with examples where corresponding sides are in proportion but the figures are not similar as long as there are more than three sides to the polygon (and, of course, if the polygons have the same number of sides).

Regardless of what they were trying to do, the authors had a very weak grasp of the concept of corresponding sides and that's a pretty scary thought given that they were writing a lesson on similarity.

Eureka Math Tips for Parents -- well, that clears up everything

Back to the language of Eureka Math thread.

I previously made the distinction between inaccuracies that come from oversimplifying a concept (particularly by using less precise, nontechnical language) and those that come from not understanding that concept. The first type is regrettable but occasionally unavoidable (at least in lower level classes); there is no real excuse for the second.

When writers make mistakes while explaining technical concepts with non-technical language, it can be often be difficult to decide which kind of mistake they're making (think Malcolm Gladwell). If, on the other hand, the writers drag the readers through impenetrable technical explanations and still get things wrong...

We've already established that there are lots of mistakes in the Eureka Math materials (with more examples to come), but it's important to note that the mistakes we are talking about do not come from oversimplifying the concepts or making them accessible to younger learners. Instead the lessons are often filled with formal and painfully dense mathematical explanations.

Here's an example from the parent section of Eureka Math ("a suite of tools that will help you to help your child learn more"). Keep in mind, the target audience is parents who are having trouble with the homework their eighth graders are bringing home.

Check this one out.

Here's a more readable version (at least in terms of font size):

Dilation: A transformation of the plane with center O and scale factor r(r > 0). If
D(O) = O and if P ≠ O, then the point D(P), to be denoted by Q, is the point on the ray OP so that |OQ| = r|OP|. If the scale factor r ≠ 1, then a dilation in the coordinate plane is a transformation that shrinks or magnifies a figure by multiplying each coordinate of the figure by the scale factor.

Congruence: A finite composition of basic rigid motions—reflections, rotations,
translations—of the plane. Two figures in a plane are congruent if there is a congruence that maps one figure onto the other figure.

Similar: Two figures in the plane are similar if a similarity transformation exists, taking one figure to the other.

Similarity Transformation: A similarity transformation, or similarity, is a composition of a finite number of basic rigid motions or dilations. The scale factor of a similarity transformation is the product of the scale factors of the dilations in the composition; if there are no dilations in the composition, the scale factor is defined to be 1.

Similarity: A similarity is an example of a transformation.

This wouldn't be A-level work in a graduate math class (I had to read through this a couple of times before I realized that O was supposed to be the center of dilation. Dangling modifiers are a bad idea in a formal definition), but the language would be appropriate. For the target audience, though, you might as well be speaking Sanskrit.

If you're reading this, it's likely you're a math person, and there's a good chance you've taken classes like abstract algebra and real analysis. If so, I'd like you to try a bit of sympathetic imagination and put yourself in the place of someone who struggles to understand the eighth grade math homework his or her children bring home. Now go back and read this section.

I can't imagine anyone who actually needs help getting anything out of this, while the people who can follow these definitions could probably do a better job writing them on their own.

[Later in the same PDF, the authors make an appalling mistake explaining corresponding sides, but that's a topic for another post.]

Problems with Common Core and EngageNY -- statistics edition

Last week we came back to the topic of Common Core standards thanks to this extraordinary post by Gary Rubinstein which uncovered some appalling quality control issues.

The problems involved EngageNY (arguably the gold standard in CC based lesson plans). Rubinstein focused on algebra; I decided to check out the sections on statistics. What I found was uniformly bad. I’m going to focus one section [Lesson 30:  Evaluating Reports Based on Data from an Experiment], but the general concerns apply to all of the sections I looked at.

When explaining a highly technical subject to younger students, we sometimes go too far in an effort to smooth off the edges. We lose precision trying to stick with everyday language and we leave out important details because they greatly complicate the picture. When we try to communicate scientific concepts, there will always be a trade-off between being accurate and being understandable.

This is invariably a judgment call. What's more, it is a judgment call that varies from subject to subject and from audience to audience. We can argue about where exactly to make the cut, but we can’t really say one position is right and the other is wrong.

That’s not what we’re talking about with EngageNY. The authors like to throw in impressive-sounding scientific language and wordy constructions but not in a way that makes the writing more precise.

For example:

Students should look to see if the article explicitly states that the subjects were randomly assigned to each treatment group.  This is important because random assignment negates the effects of extraneous variables that may have an effect on the response by evenly distributing these variables into both treatment groups.

“[N]egates the effects of extraneous variables that may have an effect” is not a phrase that the typical high school student will find particularly informative, but this paragraph also manages to be not-quite right. That “evenly” seems to suggest that the distribution (rather than the expected distributions) of non-treatment variables will be identical, while the part about “distributing” variables just seems odd.

At best, these lessons are sloppy; at worst, they’re wrong. Take this for example:

Suppose newspaper reporters brainstormed some headlines for an article on this experiment.  These are their suggested headlines:

A. “New Treatment Helps Pericarditis Patients”
B. “Colchicine Tends to Improve Treatment for Pericarditis”
C. “Pericarditis Patients May Get Help”

7. Which of the headlines above would be best to use for the article?  Explain why.

Headline A would be the best because this is a well-designed experiment.  Therefore, a cause and effect relationship has been established.  Headlines B and C talk about a tendency relationship, not a cause and effect relationship.

“Tends to improve” implies a causal relationship, as does “help” in this context. The authors appear to have confused “causal” with “deterministic.”

The quality issues we see associated with the implementation of Common Core bear a striking resemblance to the problems noted by Richard Feynman when critiquing the New Math reforms of the Sixties.

The reason was that the books were so lousy. They were false. They were hurried. They would try to be rigorous, but they would use examples (like automobiles in the street for "sets") which were almost OK, but in which there were always some subtleties. The definitions weren't accurate. Everything was a little bit ambiguous -- they weren't smart enough to understand what was meant by "rigor." They were faking it. They were teaching something they didn't understand, and which was, in fact, useless, at that time, for the child.

More fun with Common Core and exponents

After the last post, I decided to follow some of the links Gary Rubinstein provided to see if the other lessons covering exponents were as bad as the examples he chose.

See for yourself.

In case the print is too small...

Common Core -- "and the brains of Isadora Duncan"

Mathematics educator and blogger Gary Rubinstein has been doing some extraordinarily important work on the Common Core beat. There's a lot of confusion about the boundaries of the discussion, and they have a way of shifting between and sometimes even within arguments.

A great deal of that shifting centers around exactly what constitutes Common Core. Proponents will often fall back to the "just a set of standards" definition and claim that criticisms involving implementation are invalid. That's a difficult position to hold since the standards without implementation aren't that meaningful, particularly considering that schools already have state or district standards in place that aren't all that different from Common Core.

A much more tenable defense is that the bad examples circulating online aren't really aligned with Common Core and we should wait until there's a faithful implementation before judging. This is the argument Rubinstein goes after, starting with this analysis by Education Week.

[Eureka Math is more or less the same as EngageNY. I'm still looking for an official statement but you can pretty much use them interchangeably.]

I volunteer with an after school tutoring program here in LA.in a program that largely focuses on language arts, my role is designated math guy. I go from table to table answering any algebra/geometry/calculus questions that that the regular tutors can't handle. Sometimes this is because the tutors have forgotten what similar triangles are or how to apply the quadratic formula, but just as often, the problem has less to do with math and more to do with Common Core. It is not unusual for a volunteer who happens to be an engineer or a computer scientist to wave me over because he or she has no idea what the question is asking. In these cases, I noticed that the EngageNY logo often appeared at the bottom of the worksheet.

Rubinstein has dug deeply into the EngageNY materials being given to students and what he has found is not good.

First of all, some lessons are full of errors.  Second, some lessons are unnecessarily boring, and third, some lessons are unnecessarily confusing.

I should note that I have not gone through every module in every grade.  I also did not search through to cherry pick examples that were particularly bad.  I just randomly picked some important topics to see how they covered them and either I just happened to find the only four bad lessons in my first four tries or there are so many flawed lessons in this project that randomly selecting a bad one is quite likely.  It’s a bit like evaluating a singer and the first few songs you listen to are out of tune.  How many more do you have to listen to before you can safely assume that this is not someone with a lot of talent?

Exhibit A is the first lesson in the first module for 8th grade, exponents.  On the second page, they introduce the concept of raising a negative number to a positive integer.  Every real math teacher knows that there is a difference between the two expressions (-2)^4 and -2^4.  The first one means (-2)*(-2)*(-2)*(-2)=+16 while the second one, without the parentheses around the -2 means -1*2*2*2*2=-16.  I have checked with all the math teachers I know, and none have ever seen -2^4 interpreted as (-2)^4.  Yet, here all over lesson one module one for 8th grade EngageNY teacher’s edition, we see this mistake.

And from the 8th grade EngageNY teacher’s edition

According to Rubinstein, this mistake is made eighteen out of the twenty times the topic is addressed.

I'll be coming back to this later but for now I'm going to close with a couple of paragraphs from the my Monkey Cage piece on Common Core and the New Math of the Sixties.

One of the best summaries of these criticisms came from Pólya, who alluded to the famous, though probably apocryphal, story of Isadora Duncan suggesting to George Bernard Shaw that they should have a child because it would have her beauty and his brains, to which Shaw is supposed to have replied that it could well have her brains and his beauty.

Pólya suggested that new math was somewhat analogous to Duncan’s proposal. The intention had been to bring mathematical researchers and high school teachers together so that the new curriculum would combine the mathematical understanding of the former and the teaching skills of the latter, but the final product got it the other way around.

The sad part is this time they found someone with far less mathematical understanding than the high school teachers.

Like I told you...

SOH, CAH, TOA is a lousy mnemonic device.

Make sure to downplay the numerology, but...

... as a number game, this might be fun for the younger kids and since these ads are from the post-war era, there might be a teaching across the curriculum opportunity here.

From A Statistician Walks into a Grocery Store...

Of course, given the junk food sponsor, you might want to do a bit of editing.

Invertibles

From Classic Puzzles for the Classroom:

The invertible, a picture that depicts one thing when held right side up and another when held upside down, was one of the most popular features of the comics puzzle page. From a puzzle standpoint it is an odd beast, being perhaps closer to an optical illusion than a true puzzle for the reader (though arguably not for the creator).

Perhaps the most impressive use of the form was made by turn-of-the-century artist Gustave Verbeek who produced a weekly invertible comic strip. In Verbeek’s world, a fish attacking a canoe in panel 5…

Might become a giant Roc in panel 8.

Here is another sample of Verbeek’s work followed by some of the invertibles you would have seen in Golden Age comics.

Puzzle Wednesdays

Worth Carnahan is one of those Golden Age artists who has fallen into near complete obscurity despite some very good work. For the next few weeks, we'll take a look at some of the puzzle pages he did for Harvey's Champion Comics.

Here's number 7  and the last in the series. Check back next week for more puzzles.

From Classic Puzzles for the Classroom

OOPS! -- "Mathematics can only be understood backwards but it must be proved forward" isn't ready yet

For those who came by earlier, I apologize. I hit 'publish' when I should have hit 'save.'

Puzzle Wednesdays

Worth Carnahan is one of those Golden Age artists who has fallen into near complete obscurity despite some very good work. For the next few weeks, we'll take a look at some of the puzzle pages he did for Harvey's Champion Comics.

Here's number 6 in the series (sorry about the damage). Check back next week for another edition and the answers to these puzzles.

From Classic Puzzles for the Classroom

Puzzle Wednesdays

Worth Carnahan is one of those Golden Age artists who has fallen into near complete obscurity despite some very good work. For the next few weeks, we'll take a look at some of the puzzle pages he did for Harvey's Champion Comics.

Here's number 5 in the series. Check back next week for another edition and the answers to these puzzles.

From Classic Puzzles for the Classroom