A blog of tips and recommendations for anyone interested in learning or teaching mathematics.
Thursday, December 18, 2014
Rules of Kruzno -- updated
I've been alluded quite a bit to Kruzno, a game I developed a few years ago and which I am currently selling on Amazon, but I don't think I've ever posted the rules so here they are.
[Just to be clear, When you jump over a piece that you don't capture (for example, a white rook jumping a black rook), the piece that you jumped stays on the board.]
Sunday, December 14, 2014
Hexagonal chess
As mentioned before,I recently opened an Amazon store for the board game Kruzno. The game was configured to be suitable for a wide range of games. The best known of these was probably developed by Wladyslaw Glinksi in 1936. Glinski's Chess is one of the most popular chess variants with more than a half million players worldwide.
You can find rules many places online, but the following should be enough to get you started.
You can find rules many places online, but the following should be enough to get you started.
Monday, December 8, 2014
Agon
[I recently opened an Amazon store for the board game Kruzno. One of the considerations when developing the game was to configure the so that it could serve as a good utility player, suitable for a wide range of games. My favorite of these non-Kruzno games is probably Agon. It's a challenging but easy to learn game that's deserves a much bigger following. Here is the write-up I did of the rules a few years ago. You can play it on a Kruzno board, of course, but any standard hex board will do.]
Agon may be the oldest abstract strategy game played on a 6 by 6 by 6 hexagonally tiled board, first appearing as early as the late Eighteenth Century in France. The game reached it greatest popularity a hundred years later when the Victorians embraced it for its combination of simple moves and complex strategy.
The Pieces: Each player has one queen and six pawns a.k.a. guards placed in the pattern indicated below

The Objective: To place your queen in the center hexagon and surround her with all six of her guards.(below)


Moves: Think of the Agon board as a series of concentric circles (see above). Pieces can move one space at a time either in the same ring or the ring closer to the center. In the figure on the left, a piece on a hexagon marked 4 could move to an adjacent hexagon marked either 4 or 3. Only the queen is allowed to move into the center hexagon. The figure below shows possible moves.

Capturing: A piece is captured when there are two enemy pieces on either side of it. The player with the captured piece must use his or her next move to place the captured piece on the outside hexagon.
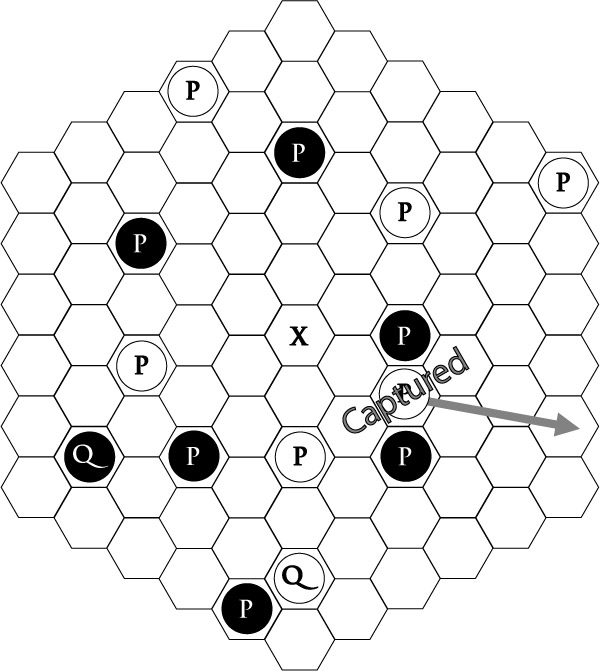
If the captured piece is a guard, the player whose piece was captured can choose where on the outer hex to place the piece. If the piece is a queen, the player who made the capture decides where the queen should go.
If more than one piece is captured in one turn, the player whose pieces were captured must move them one turn at a time.
If a player surrounds the center hexagon with guards without getting the queen into position, that player forfeits the game.
Agon may be the oldest abstract strategy game played on a 6 by 6 by 6 hexagonally tiled board, first appearing as early as the late Eighteenth Century in France. The game reached it greatest popularity a hundred years later when the Victorians embraced it for its combination of simple moves and complex strategy.
The Pieces: Each player has one queen and six pawns a.k.a. guards placed in the pattern indicated below

The Objective: To place your queen in the center hexagon and surround her with all six of her guards.(below)


Moves: Think of the Agon board as a series of concentric circles (see above). Pieces can move one space at a time either in the same ring or the ring closer to the center. In the figure on the left, a piece on a hexagon marked 4 could move to an adjacent hexagon marked either 4 or 3. Only the queen is allowed to move into the center hexagon. The figure below shows possible moves.

Capturing: A piece is captured when there are two enemy pieces on either side of it. The player with the captured piece must use his or her next move to place the captured piece on the outside hexagon.

If the captured piece is a guard, the player whose piece was captured can choose where on the outer hex to place the piece. If the piece is a queen, the player who made the capture decides where the queen should go.
If more than one piece is captured in one turn, the player whose pieces were captured must move them one turn at a time.
If a player surrounds the center hexagon with guards without getting the queen into position, that player forfeits the game.
Wednesday, November 26, 2014
Effort and Results
If we want to be serious about improving education, one of the first things we need to think about is the real and perceived relationship between effort and results. Take a look at the following three cases. To keep the discussion simple, I am using unrealistically idealized curves, but they should illustrate the main principles.
Let's say that the X axis in the graph above represents days in the semester and the Y axis represents some measure of mastery.
Which of these learning would we like to see?
It is easy enough to eliminate C. Obviously we don't want kids getting frustrated by going most of the semester without any progress .
Of the remaining two, most people would probably choose A, but I am going to strongly argue for B. I want to see B because I want the students to expect B in the future. I want them to go into every new topic believing that they probably won't see much if any progress at first but eventually they will see a more-or-less linear relationship between the work they put in and what they get out of it.
The great problem with A is that it reinforces students' most dangerous misconception: that math is something you get or you don't; that understanding either comes quickly or it doesn't come at all. You simply can't motivate people to work hard when they believe that work is futile.
Let's say that the X axis in the graph above represents days in the semester and the Y axis represents some measure of mastery.
Which of these learning would we like to see?
It is easy enough to eliminate C. Obviously we don't want kids getting frustrated by going most of the semester without any progress .
Of the remaining two, most people would probably choose A, but I am going to strongly argue for B. I want to see B because I want the students to expect B in the future. I want them to go into every new topic believing that they probably won't see much if any progress at first but eventually they will see a more-or-less linear relationship between the work they put in and what they get out of it.
The great problem with A is that it reinforces students' most dangerous misconception: that math is something you get or you don't; that understanding either comes quickly or it doesn't come at all. You simply can't motivate people to work hard when they believe that work is futile.
Wednesday, November 12, 2014
Fixing Common Core*
* or at least a small part thereof.
Last week I opened up a thread on what's wrong with many of the homework problems appearing under the banner of Common Core (if you click on the link, make sure to check out the comment section). The post included an example that's been bouncing around the internet for a while.
In this post, I'll drill a little deeper into the problem and discuss what the authors were probably trying to do, how they screwed up and what could be done to fix it.
The offending problem reads as follows:
4. Steven solves 7 x 3 using the distributive property. Show an example of what Steven's work might look like below.
I shared this problem with an engineer, a physicist and a statistician. All three had Ph.D.s and extraordinary analytic chops, but none of them got the problem (the engineer came the closest with a tentative "Surely they don't want you to..."). It wasn't that they didn't understand the mathematics; it was that they understood it too well. What threw them was that using the distributive property was such a silly choice in this context. Once the problem was changed slightly so that the approach made sense, all three got it immediately.
I'll discuss that tweak in a minute, but first, let's talk about what the problem was trying to do.
The idea that the creators are going after both here and in many other problems is that there are different ways of stating the same number. For example, we can think of nine simply as nine or as ten minus one or as three square or as 900% or any other number of ways.
Unfortunately, there is a second equally important part to this idea that the authors generally mishandle or leave out completely: we want to find the form of the number that makes the problem easiest.
It's true that 7x3 = 5x3 + 2x3 = 10x3 - 3x3 but there's no good reason to do the problem those ways. The students have very probably learned their multiplication tables by this point and even if they haven't, it's easier just to add 7+7+7.
So, how can we fix this problem?
For starters, we need to think about what is bookable. Some things are simply better explained in person and left out of assignments the students do on their own.
If we do decide that this is a concept we want to cover extensively in homework, we have to make sure that we are clearly and logically explaining what's going on. This is a particularly weak point in many Common Core based materials. Not only do the worksheets have incredibly inadequate explanations; the books are often even worse.
Finally and perhaps most importantly, we need to set up the problems so that the technique we are trying to teach makes sense.
There is no good reason to use the distributive property to multiply 7×3. There is, however, a not bad reason for using the distributive property to multiply 19×3 and a pretty good reason to use the distributive property to multiply 98×3 and a very good reason to use the distributive property to multiply 998×3.
If you try to do these problems in your head, you will probably find that it's much easier to think of them as
3(20 - 1)
3(100 - 2)
3(1000 - 2)
After tweaking, these problems not only illustrate the technique, they put it in an appropriate context.
This is, of course, a single example but it's consistent with what I've been seeing while helping students from various grades.with their math homework. A large number of the problems I see are so bad as to suggest either extreme carelessness or a profound lack of understanding of what the problems are supposed to accomplish.
p.s. I've also been writing on this topic at West Coast Stat Views for awhile now. You can see a collection of education reform posts here or you can just go to the site and search on 'education'.
Monday, November 10, 2014
The unbookable lesson
Have you ever seen the original Flight of the Phoenix? If not you might want to skip the rest of this paragraph. The plot involves a group of men trying to rebuild a plane that crashed in the middle of the desert. The plan for the reconstruction comes an arrogant engineer who assures them that he has designed many planes in the past. It is only near the end of the project that the rest of the men learn that engineer only designed model planes that had, at best, flown a few hundred yards. Upon learning that their fate depends on someone who, in their words, makes "toy planes," the men are understandably despondent but the engineer argues that it actually requires more skill to design a plane that doesn't have a pilot.
You can draw an analogy with different educational media. There's a naive view of teaching that's surprisingly popular among 'thought leaders' like Thomas Friedman (and yes, I do have to use quotes whenever I use the phrase 'thought leader'). It reduces instruction to the words and pictures presented to the students. This is analogous to the idea that you could build a completely autonomous plane just by recording everything a pilot did on one flight then attaching servomotors to the controls and having them replicate all of the actions.
Good teaching is always an interactive process, though the interactions may not always be readily apparent to the casual observer. Even when you aren't actively answering questions or soliciting feedback, being an effective instructor means constantly reading your audience. You have to be alert to expressions and body language. If you see nodding and looks of relief, you might want to speed up. If you see wide eyes and slack faces, you probably need to slow down, add a simpler example, or even go back and start the lesson over..
After you do teach for a while, you will find that when you do ask questions or open up the floor, you will already have a remarkably good idea of where the kids are having problems.
If you take away that feedback channel, things become radically different, almost always for the worse. Explanations that seemed perfectly clear to the class in person will seem incomprehensible when presented over a YouTube video. Lessons that worked beautifully in the classroom will leave students confused and angry if done online.
This all ties closely to the concept of bookable instruction, classroom lessons that lends themselves to adaptation to books and other non-interactive media. Most history lessons are fairly bookable; almost no math lessons are.
When it comes to educational technology, the medium is very much a part of the message. Unfortunately, it’s a part that has been all but completely lost amid all of the hype over MOOCs and iPads.
You can draw an analogy with different educational media. There's a naive view of teaching that's surprisingly popular among 'thought leaders' like Thomas Friedman (and yes, I do have to use quotes whenever I use the phrase 'thought leader'). It reduces instruction to the words and pictures presented to the students. This is analogous to the idea that you could build a completely autonomous plane just by recording everything a pilot did on one flight then attaching servomotors to the controls and having them replicate all of the actions.
Good teaching is always an interactive process, though the interactions may not always be readily apparent to the casual observer. Even when you aren't actively answering questions or soliciting feedback, being an effective instructor means constantly reading your audience. You have to be alert to expressions and body language. If you see nodding and looks of relief, you might want to speed up. If you see wide eyes and slack faces, you probably need to slow down, add a simpler example, or even go back and start the lesson over..
After you do teach for a while, you will find that when you do ask questions or open up the floor, you will already have a remarkably good idea of where the kids are having problems.
If you take away that feedback channel, things become radically different, almost always for the worse. Explanations that seemed perfectly clear to the class in person will seem incomprehensible when presented over a YouTube video. Lessons that worked beautifully in the classroom will leave students confused and angry if done online.
This all ties closely to the concept of bookable instruction, classroom lessons that lends themselves to adaptation to books and other non-interactive media. Most history lessons are fairly bookable; almost no math lessons are.
When it comes to educational technology, the medium is very much a part of the message. Unfortunately, it’s a part that has been all but completely lost amid all of the hype over MOOCs and iPads.
Friday, November 7, 2014
A step-up SAT/GRE problem -- Circles (Rhombus edition)
In an earlier post, we talked about "step-back problems." The idea is that, wherever possible, each problem should be associated with at least one problem that uses similar format and relies on similar concepts but which "steps up" (is more difficult) or "steps down" (is easier).
In that previous post we talked about problems where you had to find the shaded area of a circle. This problem covers similar territory but takes things up a notch.
Circle 1 and Circle 2 both have radius 2. Each passes through the center of the other. Find the area of the rhombus formed by the two points of intersection (A and B) and the centers of each circle (C1 and C2).
Solution after the break.
In that previous post we talked about problems where you had to find the shaded area of a circle. This problem covers similar territory but takes things up a notch.
Circle 1 and Circle 2 both have radius 2. Each passes through the center of the other. Find the area of the rhombus formed by the two points of intersection (A and B) and the centers of each circle (C1 and C2).
Solution after the break.
Thursday, November 6, 2014
Deconstructing Common Core
[A quick note: there's been some confusion over over exactly what constitutes Common Core, I might dig deeper into the question at a later date, but for this post, we'll be talking about materials released under the Common Core banner.]
I volunteer a couple of times a week to help a group that tutors kids from urban schools. My role is designated math guy. I go from table to table helping kids with the more challenging homework problems.
Recently, I have noticed a pattern in helping with Common Core problems. First I explained them to the students, then I explained them to the tutors.
That may be the most noticeable difference between the mathematics of Common Core and the new math of the 60s. In the summer of love, an advanced degree in mathematics or engineering was sufficient to understand an elementary school student's homework. These days, the tutors with math backgrounds often find themselves more confused than their less analytic counterparts since what they know about solving the problem seems to have nothing to do with what the assignment asks for.
To follow a Common Core worksheet, you really need to have a little knowledge of the underlying pedagogical theories. Unfortunately, if you have more than a little knowledge, you'll find these worksheets extraordinarily annoying because, to put it bluntly, much of what you see was produced by people who had a very weak grasp of the underlying concepts.
I'm starting a thread called "Fixing Common Core." I'm going to take some problems that are associated with Common Core and try to explain both what the authors were trying to do and how they could have done better with a different approach. The posts almost certainly won't live up to the title but they will, hopefully, shed some light on the topic.
I'll be back early next week with a discussion of the following:
I volunteer a couple of times a week to help a group that tutors kids from urban schools. My role is designated math guy. I go from table to table helping kids with the more challenging homework problems.
Recently, I have noticed a pattern in helping with Common Core problems. First I explained them to the students, then I explained them to the tutors.
That may be the most noticeable difference between the mathematics of Common Core and the new math of the 60s. In the summer of love, an advanced degree in mathematics or engineering was sufficient to understand an elementary school student's homework. These days, the tutors with math backgrounds often find themselves more confused than their less analytic counterparts since what they know about solving the problem seems to have nothing to do with what the assignment asks for.
To follow a Common Core worksheet, you really need to have a little knowledge of the underlying pedagogical theories. Unfortunately, if you have more than a little knowledge, you'll find these worksheets extraordinarily annoying because, to put it bluntly, much of what you see was produced by people who had a very weak grasp of the underlying concepts.
I'm starting a thread called "Fixing Common Core." I'm going to take some problems that are associated with Common Core and try to explain both what the authors were trying to do and how they could have done better with a different approach. The posts almost certainly won't live up to the title but they will, hopefully, shed some light on the topic.
I'll be back early next week with a discussion of the following:
Sunday, November 2, 2014
I had a post in mind for this clip...
But I forget what I was going to say...
Still a great scene, though.
Monday, October 27, 2014
A logic puzzle clue trading game
I've been on a logic puzzle binge recently (all in the name of research, of course) and I got to thinking about some games that could be built around the puzzles.
Just to review, here's a description from Wikipedia:
Here are some potential rules:
1. Each clue is printed on a separate card;
2. An equal number of cards are dealt to each team. Remaining cards are turned face up for everyone to see;
3. Teams take turns filling in cells with x's and o's. There is no limit to the number of cells that can be filled in a single turn.Teams receive one point for every correct x and ten points for every correct o. Incorrect guesses cause a team to lose a turn. If the incorrect guess was an o and the cell was actually an x, the moderator fills in that one cell. If the incorrect guess was an x and the cell was actually an o, the moderator will fill in the o-cell and will put x's in the cells of the row and column containing the o.
4. After each turn, the team that just went will have a chance to trade cards with other teams. Teams must describe their cards honestly though they can withhold information. For example "Our card involves Alice and honey" could describe the clue "Alice ate the honey" or "Alice did not eat the honey" or "Either Alice ate the honey or Simon ate the jam."
5. Teams can copy clues before trading them away.
Still very much in the early stages. Let me know if you can come up with something better.
Just to review, here's a description from Wikipedia:
Another form of logic puzzle, popular among puzzle enthusiasts and available in magazines dedicated to the subject, is a format in which the set-up to a scenario is given, as well as the object (for example, determine who brought what dog to a dog show, and what breed each dog was), certain clues are given ("neither Misty nor Rex is the German Shepherd"), and then the reader fills out a matrix with the clues and attempts to deduce the solution. These are often referred to as "logic grid" puzzles. The most famous example may be the so-called Zebra Puzzle, which asks the question Who Owned the Zebra?.
Here are some potential rules:
1. Each clue is printed on a separate card;
2. An equal number of cards are dealt to each team. Remaining cards are turned face up for everyone to see;
3. Teams take turns filling in cells with x's and o's. There is no limit to the number of cells that can be filled in a single turn.Teams receive one point for every correct x and ten points for every correct o. Incorrect guesses cause a team to lose a turn. If the incorrect guess was an o and the cell was actually an x, the moderator fills in that one cell. If the incorrect guess was an x and the cell was actually an o, the moderator will fill in the o-cell and will put x's in the cells of the row and column containing the o.
4. After each turn, the team that just went will have a chance to trade cards with other teams. Teams must describe their cards honestly though they can withhold information. For example "Our card involves Alice and honey" could describe the clue "Alice ate the honey" or "Alice did not eat the honey" or "Either Alice ate the honey or Simon ate the jam."
5. Teams can copy clues before trading them away.
Still very much in the early stages. Let me know if you can come up with something better.
Friday, October 17, 2014
Hexagonal Reversi
Now that you have a hexboard, here's on of many games you can play on it. Hexagonal Reversi is very similar to regular Reversi (which is suspiciously similar to Othello, but that's a subject for another post).
Here are the starting positions:
Each player takes turns placing one of his or her pieces on the board so that at least one row of the opponent's pieces lie between the newly placed piece and another piece already on the board at which point the row of opponent's pieces are replaced with the player's pieces.
This figure above shows the possible initial moves if black goes first (B) or if white goes first (W).
Here are the starting positions:
Each player takes turns placing one of his or her pieces on the board so that at least one row of the opponent's pieces lie between the newly placed piece and another piece already on the board at which point the row of opponent's pieces are replaced with the player's pieces.
This figure above shows the possible initial moves if black goes first (B) or if white goes first (W).
Wednesday, October 15, 2014
Make your own hexagonal game board
After the standard 8x8 chess board, the 6x6x6 hexboard might be the most versatile piece of equipment an abstract strategy gamer can own. (Here are a few of the games you can play with this set.)
If you're serious about games you should probably buy one of the boards, but if money's tight or if you want to ease your way in, here's a good, high-res image that you can download and print off to make your own.
If you're serious about games you should probably buy one of the boards, but if money's tight or if you want to ease your way in, here's a good, high-res image that you can download and print off to make your own.
Tuesday, October 14, 2014
Positive steps: if we have to make tough choices then we need to be honest about them
A few years ago I taught at a small rural school in the Mississippi Delta. The old timers would talk at great length about how much better the school had been before I got there. They attributed the decline to the closing of the alternative school. In the "good old days," any student who caused trouble would be pulled out of class and sent to a special, highly structured school -- basically a glorified study hall -- run by an honest-to-God former Marine drill sergeant.
According to the version I was told, the program worked exceptionally well but was shut down in a discrimination suit because a disproportionate number of African-American students were being sent to there. This was a very conservative community (I doubt that there was a unionized teacher in the county let alone in the school), so it is not surprising that this was seen as another instance of the federal government interfering.
As you might guess, I saw things a bit differently. The government has not only the right but the obligation to step in in cases of racial discrimination. Furthermore, even if there had not been a civil rights issue here, I still have very mixed feelings about policies that potentially denied certain kids a quality education simply because they were difficult to deal with.
There is, of course, another side to the debate. In a world of fixed resources, educators frequently have to weigh the needs of the many against the needs of the few. If a small group of students is undermining the quality of education for the student body as a whole, there is a case to be made for removing the students. Just as importantly, sometimes that particular disciplinary action is the best thing for the kid being disciplined. For some, the structure and discipline of a boot camp environment really is the best educational setting. For others, there is a scared-straight effect. For these kids, a brief stay in the alternative school is enough to convince them to improve their behavior and work habits.
There are a lot of lessons to be learned here, but for me, the big one is that education is filled with tough choices and difficult trade offs. We need to acknowledge this difficulty. We need to have honest, well thought out discussions about the consequences of discipline and expulsion (both nominal and de facto). In particular, if we decide to sacrifice one student for the good of the many, we need to own up to that decision.
Today, in many schools, we have covert policies in place (particularly in the popular "no excuses" schools) that effectively mimic the alternative school approach of that small Delta town, including having a disproportionate impact on African-American males (often taking it to the next degree). But as much as that troubles me, what bothers me even more is the fact that we don't face up to what we're doing.
According to the version I was told, the program worked exceptionally well but was shut down in a discrimination suit because a disproportionate number of African-American students were being sent to there. This was a very conservative community (I doubt that there was a unionized teacher in the county let alone in the school), so it is not surprising that this was seen as another instance of the federal government interfering.
As you might guess, I saw things a bit differently. The government has not only the right but the obligation to step in in cases of racial discrimination. Furthermore, even if there had not been a civil rights issue here, I still have very mixed feelings about policies that potentially denied certain kids a quality education simply because they were difficult to deal with.
There is, of course, another side to the debate. In a world of fixed resources, educators frequently have to weigh the needs of the many against the needs of the few. If a small group of students is undermining the quality of education for the student body as a whole, there is a case to be made for removing the students. Just as importantly, sometimes that particular disciplinary action is the best thing for the kid being disciplined. For some, the structure and discipline of a boot camp environment really is the best educational setting. For others, there is a scared-straight effect. For these kids, a brief stay in the alternative school is enough to convince them to improve their behavior and work habits.
There are a lot of lessons to be learned here, but for me, the big one is that education is filled with tough choices and difficult trade offs. We need to acknowledge this difficulty. We need to have honest, well thought out discussions about the consequences of discipline and expulsion (both nominal and de facto). In particular, if we decide to sacrifice one student for the good of the many, we need to own up to that decision.
Today, in many schools, we have covert policies in place (particularly in the popular "no excuses" schools) that effectively mimic the alternative school approach of that small Delta town, including having a disproportionate impact on African-American males (often taking it to the next degree). But as much as that troubles me, what bothers me even more is the fact that we don't face up to what we're doing.
Sunday, October 12, 2014
A couple of Halloween themed word puzzles
Both of these puzzles are simple enough for elementary school students but can be surprisingly challenging, even for adults.
I'd recommend having kids work on the first individually and the second as a group.
From Classic Word Problems for the Classroom.
I'd recommend having kids work on the first individually and the second as a group.
From Classic Word Problems for the Classroom.
Friday, October 10, 2014
A note on creating geometric graphics
As you can see in the previous post, I've been working on a project involving the kind of problems you might see on the SAT or GRE. I've been focusing on geometry to start with which means I have to create lots of geometric drawings.
I recently started using Inkscape and I would highly recommend it for the following reasons:
It's a free, open-source program;
It works with Scalable Vector Graphics (SVG). Scalability is a great feature;
It's easy.
Quick tip: you can draw circles and squares from a center point using the shift key.
I recently started using Inkscape and I would highly recommend it for the following reasons:
It's a free, open-source program;
It works with Scalable Vector Graphics (SVG). Scalability is a great feature;
It's easy.
Quick tip: you can draw circles and squares from a center point using the shift key.
Tuesday, October 7, 2014
A step-back SAT/GRE problem -- Circles
I've been thinking a lot about video learning, particularly video-assisted self-study. One of the ideas I've come up with is the step-back problem.
Sometimes, when you're trying to teach yourself a subject or study for a test like the SAT or GRE, you will run into a problem that still confuses you after you've gone through the explanation. If you have access to a live instructor, you can always ask for a more detailed explanation but what do you do if you are trying to learn the subject from YouTube videos?
My thought is to pair up problems of medium to high difficulty with problems that use some of the same concepts but are much simpler.
Here's an example. The following is very similar to some problems you are likely to see on the SAT or GRE. Try it on your own then check below the fold for the answer. If you didn't get the right answer and still don't understand what you got wrong even after reading the explanation, try the second problem.
The radius of circle 1 is 5. Both line segments pass through the center of the circle. Find the area of the shaded region.
Sometimes, when you're trying to teach yourself a subject or study for a test like the SAT or GRE, you will run into a problem that still confuses you after you've gone through the explanation. If you have access to a live instructor, you can always ask for a more detailed explanation but what do you do if you are trying to learn the subject from YouTube videos?
My thought is to pair up problems of medium to high difficulty with problems that use some of the same concepts but are much simpler.
Here's an example. The following is very similar to some problems you are likely to see on the SAT or GRE. Try it on your own then check below the fold for the answer. If you didn't get the right answer and still don't understand what you got wrong even after reading the explanation, try the second problem.
Circle 1
The radius of circle 1 is 5. Both line segments pass through the center of the circle. Find the area of the shaded region.
Monday, October 6, 2014
Classic Puzzles for a Monday
Given the quantity of Nugent's output, the quality was exceptionally good.
From Classic Puzzles for the Classroom.
Friday, October 3, 2014
Advice to a student about online videos --too easy is better than too difficult.
I think as a general rule, there is a lot to be said for the idea of taking the time to get the basics down and understand the fundamentals before moving on. In the context of a confused student looking to catch up, however, this rule goes from generally good to absolutely essential. The kids who are likely to seek out this kind of assistance and, more to the point, those who really need it are almost without exception afraid of the material. This anxiety is usually one of the main obstacles to mastering their lessons
One of the great advantages of watching a math video is that it doesn't watch you back. The fear of looking dumb, of being judged, is perhaps the main reason struggling students are reluctant to ask for help. Being able to listen to an explanation or see an example in a safe and private place can be remarkably beneficial but those benefits go away quickly if that video makes the viewer feel stupid or confused.
The first requirement of any math video (or math lesson, for that matter) is that it be correct, not necessarily in the picky, get-the-jargon-right sense, but correct in the sense that the basic ideas are right and you end up where you're supposed to. A close second is that the video make the student comfortable with the material. If I'm explaining a problem to a student or group of students, I can adjust my presentation based on the reactions I'm getting. I can slow down, make an explanation more detailed, offer words of reassurance, even stop what I'm doing and switch over to a simpler problem. The video instructor can do none of these things.
That said, under the right circumstances, a video that walks a student through a problem and hits just the right level of difficulty can do a lot to build both skills and comfort level.
Here's a clip that does a pretty good job, particularly with the reassurance part.
One of the great advantages of watching a math video is that it doesn't watch you back. The fear of looking dumb, of being judged, is perhaps the main reason struggling students are reluctant to ask for help. Being able to listen to an explanation or see an example in a safe and private place can be remarkably beneficial but those benefits go away quickly if that video makes the viewer feel stupid or confused.
The first requirement of any math video (or math lesson, for that matter) is that it be correct, not necessarily in the picky, get-the-jargon-right sense, but correct in the sense that the basic ideas are right and you end up where you're supposed to. A close second is that the video make the student comfortable with the material. If I'm explaining a problem to a student or group of students, I can adjust my presentation based on the reactions I'm getting. I can slow down, make an explanation more detailed, offer words of reassurance, even stop what I'm doing and switch over to a simpler problem. The video instructor can do none of these things.
That said, under the right circumstances, a video that walks a student through a problem and hits just the right level of difficulty can do a lot to build both skills and comfort level.
Here's a clip that does a pretty good job, particularly with the reassurance part.
Saturday, September 20, 2014
Puzzling your way through the GRE -- logic edition
I was looking through a GRE sample test the other day and I came across a question that looked oddly familiar. I am not going to repeat it verbatim (not quite sure of the copyright status) but the gist was that the question gave some names and some properties associated with those names and some conditions.
After a moment, I realized that this problem reminded me of an old-fashioned logic grid puzzle.
Here's an example from a popular site:
You probably won't see a grid like this on the GRE or the SAT but you will run across the underlying concepts so if you're preparing for one of these tests, it might be worth your while to spend a little of your study time as play time with these puzzles.
After a moment, I realized that this problem reminded me of an old-fashioned logic grid puzzle.
Here's an example from a popular site:
You can eliminate pairs you know aren't true with an X, and pencil in pairs you know are related with an O. If you know, for example, that Lauren wasn't born in 1961, you can add an X in the box where the Lauren column and 1961 row meet. Similarly, if you know that Bryant was born in 1971, you can add an O in the appropriate box. Furthermore, since every option can only be used once in any given puzzle, you can eliminate the four other options for Bryant in that category (1937, 1946, 1961, 1975) and the four other options for 1971 (Anahi, Jayden, Lauren and Nikolas).
You probably won't see a grid like this on the GRE or the SAT but you will run across the underlying concepts so if you're preparing for one of these tests, it might be worth your while to spend a little of your study time as play time with these puzzles.
Tuesday, September 16, 2014
An annecdote from my teaching days -- sometimes it just takes a nudge
A few years ago, I did a stint teaching math at an urban prep in Watts. It wasn't a tough school by Watts standards (and the Watts of today isn't nearly as tough as it was twenty years ago). No school with a self-selecting student body is going to be that tough.
It was, however, academically challenging. The kids came in about a year and a half below grade level and the objective was to get almost all of them into college and by that I mean almost all of the kids who enrolled. We never resorted to the high-attrition model common in 'no-excuses' charters. We also didn't bury the the kids with work. We had to find a way to get virtually all of our students up to speed while keeping their workload reasonable.
It was a daunting assignment and when I started grading their first test, I was momentarily tempted to give up. Probably half the questions were left completely blank. I was shocked. My approach to teaching math requires a lot of one-to-one interaction so I had seen all of these kids do similar problems successfully in class.
To make matters worse, I had been very clear that I would give partial credit if the students were close or even if they showed a good understanding of the question. Even with this added incentive, they were frequently not even attempting the problems.
I wrote up a new test (treating the first as a practice run), reviewed all of the material with the class and announced one change in the grading policy. I told the class that, since a blank was the most wrong answer, a blank would get the lowest score. If the students wrote anything, including "I don't know," they would get at least a point. The closer they got the better they'd score but writing anything would get them one point out of ten.
From that point on, unless the student ran out of time, I never saw a blank, but here's the kicker: I never saw anyone write "I don't know" either. Pretty much every student attempted every problem. Furthermore they were in pretty good shape for college, good enough that a fair number of them went on to some very good outcomes, including engineering degrees at schools like UCLA and USC.
There are lots of potential take-aways here, but one seems particularly relevant to some recent discussions: learned helplessness and what we might call students' static friction. Students who are having trouble, particularly those on the wrong side of the achievement gap, often find themselves in this situation. This has both a bad and a good side. It can be extraordinarily frustrating for students and educators but often, if you can manage to nudge the student while applying the right kind of instruction and motivation, you'll see a dramatic improvement.
It was, however, academically challenging. The kids came in about a year and a half below grade level and the objective was to get almost all of them into college and by that I mean almost all of the kids who enrolled. We never resorted to the high-attrition model common in 'no-excuses' charters. We also didn't bury the the kids with work. We had to find a way to get virtually all of our students up to speed while keeping their workload reasonable.
It was a daunting assignment and when I started grading their first test, I was momentarily tempted to give up. Probably half the questions were left completely blank. I was shocked. My approach to teaching math requires a lot of one-to-one interaction so I had seen all of these kids do similar problems successfully in class.
To make matters worse, I had been very clear that I would give partial credit if the students were close or even if they showed a good understanding of the question. Even with this added incentive, they were frequently not even attempting the problems.
I wrote up a new test (treating the first as a practice run), reviewed all of the material with the class and announced one change in the grading policy. I told the class that, since a blank was the most wrong answer, a blank would get the lowest score. If the students wrote anything, including "I don't know," they would get at least a point. The closer they got the better they'd score but writing anything would get them one point out of ten.
From that point on, unless the student ran out of time, I never saw a blank, but here's the kicker: I never saw anyone write "I don't know" either. Pretty much every student attempted every problem. Furthermore they were in pretty good shape for college, good enough that a fair number of them went on to some very good outcomes, including engineering degrees at schools like UCLA and USC.
There are lots of potential take-aways here, but one seems particularly relevant to some recent discussions: learned helplessness and what we might call students' static friction. Students who are having trouble, particularly those on the wrong side of the achievement gap, often find themselves in this situation. This has both a bad and a good side. It can be extraordinarily frustrating for students and educators but often, if you can manage to nudge the student while applying the right kind of instruction and motivation, you'll see a dramatic improvement.
Wednesday, August 6, 2014
Externalizing what you worked so hard to internalize
I've been writing quite a bit on the work of George Pólya, particularly focusing on what strike me as some common misconceptions and overlooked aspects. I started with his emphasis on building self-confidence and making the experience pleasant since these things are so much at odds with the tough-talk rhetoric that has become so popular in education circles over the last few years.
Pólya also spends a great deal of time talking about the importance of "getting inside the student's head," but compared to the parts about self-confidence, I think the point here is less emotional and more cognitive. One of the main ideas of the book How to Solve It is that people who work with mathematics professionally have almost invariably mastered and internalized a number of useful problem-solving tools. Unfortunately, by internalizing these tools we have also in effect hidden them from our students.
When faced with a problem, we quickly and in many cases unconsciously run through a number of techniques that we have found over the years to be helpful. We examine the problem, determine the unknown, compare the problem to those we've encountered in the past, perhaps draw a mental picture and run through any number of similar steps before deciding on the proper strategy. To the student this gives an unrealistically linear appearance to the process, as if "let u equal X cubed minus 8 and then factor by substitution" was the first thing that popped into our mind .
Polya's point, and I think it's a profound one, is that to explain a process to someone who is unfamiliar with it, you have to be self-aware enough to explain the whole process, not just the parts you are still conscious of.
Here's a great bad example from one of our recent whipping boys.
For the math people out there, this is not a bad explanation, but we aren't the target audience. For the target audience, this just terrible, particularly for a video. If you're working live, you can read the room. With a recorded medium, you have to anticipate the room.
Think of the world as being divided into two groups: people who can do this problem without help; and people who can't. The person doing this video is obviously in the first group, For the first group, setting up equations is second nature. It's obvious me, having been through this from every vantage, that the instructor took a few seconds to understand the problem and mentally outline the steps for solving problem, then he hit record and started filling that outline in.
The trouble is, for the overwhelming majority of the people in the second group, getting that outline is the part they were having trouble with. Very seldom do you see students who can effortlessly set up the equations for a word problem but who then get stuck on the basic algebra.
The students who need help look at this problem and see a lot of possible variables and equations. Maybe X should be the amount spent on the expensive paper. Maybe we should set up an equation to show the difference between the two amounts, cheap and expensive. You and I know these are dead ends because we've seen this show before. The key to explaining this type of problem is to imagine what it would look like if you were seeing it for the first time.
George Pólya was, of course, big on word problems. Here's a relevant passage from How to Solve It:
Pólya also spends a great deal of time talking about the importance of "getting inside the student's head," but compared to the parts about self-confidence, I think the point here is less emotional and more cognitive. One of the main ideas of the book How to Solve It is that people who work with mathematics professionally have almost invariably mastered and internalized a number of useful problem-solving tools. Unfortunately, by internalizing these tools we have also in effect hidden them from our students.
When faced with a problem, we quickly and in many cases unconsciously run through a number of techniques that we have found over the years to be helpful. We examine the problem, determine the unknown, compare the problem to those we've encountered in the past, perhaps draw a mental picture and run through any number of similar steps before deciding on the proper strategy. To the student this gives an unrealistically linear appearance to the process, as if "let u equal X cubed minus 8 and then factor by substitution" was the first thing that popped into our mind .
Polya's point, and I think it's a profound one, is that to explain a process to someone who is unfamiliar with it, you have to be self-aware enough to explain the whole process, not just the parts you are still conscious of.
Here's a great bad example from one of our recent whipping boys.
For the math people out there, this is not a bad explanation, but we aren't the target audience. For the target audience, this just terrible, particularly for a video. If you're working live, you can read the room. With a recorded medium, you have to anticipate the room.
Think of the world as being divided into two groups: people who can do this problem without help; and people who can't. The person doing this video is obviously in the first group, For the first group, setting up equations is second nature. It's obvious me, having been through this from every vantage, that the instructor took a few seconds to understand the problem and mentally outline the steps for solving problem, then he hit record and started filling that outline in.
The trouble is, for the overwhelming majority of the people in the second group, getting that outline is the part they were having trouble with. Very seldom do you see students who can effortlessly set up the equations for a word problem but who then get stuck on the basic algebra.
The students who need help look at this problem and see a lot of possible variables and equations. Maybe X should be the amount spent on the expensive paper. Maybe we should set up an equation to show the difference between the two amounts, cheap and expensive. You and I know these are dead ends because we've seen this show before. The key to explaining this type of problem is to imagine what it would look like if you were seeing it for the first time.
George Pólya was, of course, big on word problems. Here's a relevant passage from How to Solve It:
Monday, August 4, 2014
Pedagogical MacGuffins
What's a MacGuffin? A MacGuffin is the key or stolen diamonds or secret code or NOC list that the characters desperately pursue. Audiences, pretty much by definition don't care about MacGuffins, but they do enjoy watching characters pursue them. Sometimes the audience isn't even clear on what the MacGuffin is.
Do you know what a NOC list is?
A pedagogical MacGuffin is a type of problem we pretend to care about even though we really don't. Like its fictional counterpart, what's important with a mathematical MacGuffin is not the thing but the pursuit.
The classic example is factoring polynomials. A standard part of most algebra classes is to learn how to take a trinomial like
2x^2 - x - 15
and find two binomials you can multiply together to get it
(2x+5)(x-3)
Every once in a great while, you'll get a trinomial that won't factor but the rest of the time you'll get a nice clean answer where each binomial consists of an integer times x plus another integer. At least, that's how it works with the assignments. You may even be told that polynomial factoring is useful because it can help you solve equations. That part is a lie.
With a couple of notable exceptions (differences between two squares and perfect square trinomials), you will probably never even try to solve a problem by factoring a quadratic for the simple reason that most don't factor.
Not only does solving by factoring usually not work; we already have a simpler method that always works, the quadratic formula.
The truth is, we don't care whether or not you know how to factor a trinomial; we care about what you learned in the pursuit, things like problem solving skills and insights into how numbers work.
(2x+5)(x-3) is just something to keep the plot moving.
If you're interested, try a few randomly generated trinomials and see how many you can get to factor.
Thursday, July 31, 2014
Slow starters -- when the race is not to the swift
In his book Mastery, George Leonard has some interesting thoughts about slow learners.
My experience as an instructor has shown me, for one thing, that the most talented students don't necessarily make the best martial artists. Sometimes, strangely enough, those with exceptional talent have trouble staying on the path of mastery. In 1987, my colleagues at Esquire and I conducted a series of interviews with athletes known as masters of their sports, which tended to confirm this paradoxical finding. Most of the athletes we interviewed stressed hard work and experience over raw talent. "I have seen so many baseball players with God-given ability who just didn't want to work," Rod Carew said. "They were soon gone. I've seen others with no ability to speak of who stayed in the big leagues for fourteen or fifteen years."
Good Horse, Bad Horse
In his book Zen Mind, Beginner's Mind, Zen master Shunryu Suzuki approaches the question of fast and slow learners in terms of horses. "In our scriptures, it is said that there are four kinds of horses: excellent ones, good ones, poor ones, and bad ones. The best horse will run slow and fast, right and left, at the driver's will, before it sees the shadow of the whip; the second best will run as well as the first one, just before the whip reaches its skin; the third one will run when it feels pain on its body; the fourth will run after the pain penetrates to the marrow of its bones. You can imagine how difficult it is for the fourth one to learn to run.
"When we hear this story, almost all of us want to be the best horse. If it is impossible to be the best one, we want to be the second best." But this is a mistake, Master Suzuki says. When you learn too easily, you're tempted not to work hard, not to penetrate to the marrow of a practice.
"If you study calligraphy, you will find that those who are not so clever usually become the best calligraphers. Those who are very clever with their hands often encounter great difficulty after they have reached a certain stage. This is also true in art, and in life." The best horse, according to Suzuki, may be the worst horse. And the worst horse can be the best, for if it perseveres, it will have learned whatever it is practicing all the way to the marrow of its bones.
Suzuki's parable of the four horses has haunted me ever since I first heard it. For one thing, it poses a clear challenge for the person with exceptional talent: to achieve his or her full potential, this person will have to work just as diligently as those with less innate ability. The parable has made me realize that ifl'm the first or second horse as an instructor of fast
Wednesday, July 30, 2014
A Tale of Three Students
Most normal people (a.k.a. non-statisticians) tend to think in linear terms. The trouble is most normal behavior doesn't tend to be very linear. As a rule, you're better off thinking in terms of of U-curves (things go either up or down then come back) and S-curves (things are level, they move either up or down, then they level off again). These are still approximations, but they are usually more reasonable approximations.
This is particularly true in education. Arguably the best way to model learning is with a series of S-curves. We work and study with little progress, then we have a period of improvement, then we hit another plateau.
If we think in terms of straight lines, ranking students is relatively easy.
But if we think in terms of S-curves, which is a great deal more realistic, things get more complicated.
The x-axis doesn't actually mean anything (this is made-up data), but let's say it represents months studying a language and the lines represent daily test scores. Now, who's the best student depends on when you ask, and that raises some troubling points.
We tend to put too much faith both in the metrics we use to evaluate students and in the linearity of human behavior. We are not straight -line animals but we have a bad habit of making straight line decisions. In this case, think of what would happen if we made a decision on who to drop from a program after two months.
Monday, July 28, 2014
The Power and Peril of Positive Thinking
Having hammered away at the importance of student self-confidence and positive attitude as a condition for success in math (part of the larger discussion of applying Pólya's teaching principles), it's important to step back and point out that a lot of people have made horrible, costly mistakes thanks to positive thinking and the influence of motivational speakers (for example).
With fantastic successes on one side and horror stories on the other, it is tempting to call this a wash, but if you think like a statistician (and you should always think like a statistician) and start breaking things down, you'll find that a few common sense rules can tell you when to assume the best and when to prepare for the worst.
Being pragmatic about being positive
For the purposes of this discussion, let's decide on a fairly precise definition of what we mean by positive thinking:
To apply positive thinking to a task, you act under the assumption that, given reasonable and intelligently applied effort, the probability of success is close to one;
Furthermore, this assumption will not be reassessed unless there is a major change in the situation.
The advantages to this approach are: we can waste a great deal of time and energy worrying; overestimating risk can cause us to prematurely abandon projects; thoughts of failure can cause us to "flinch," to hold back and not give the task our best effort. Avoiding these things can allow positive thinking to create self-fulfilling prophecies.
The disadvantages are that underestimating the probability of failure can cause us to waste resources on projects with negative expected value and, more importantly, failing to pay attention to warning signs can leave us vulnerable to otherwise avoidable disasters.
We could have a general discussion at this point about the relative weight of these advantages and disadvantages but it wouldn't be very productive because neither risk nor reward are evenly distributed. In many if not most situations, a fairly clear case can be made for either positive or cautious thinking. To determine which approach is best for a given situation, think about these rules of thumb:
Before you commit yourself, try to think realistically about the expected value in terms of other people's success rates;
Never bet more than you're willing to lose;
Consider collateral damage (are you putting your spouse and children at risk of hardship?);
Is there incremental payoff? This last one is extremely important. If you decide to start a restaurant or move to NYC to make it on Broadway, and you fail, then you will probably have very little to show for the effort. If, on the other hand, you decide to lose forty pounds through diet and exercise or to go from being a C student to an A student, then there is incremental pay off for your hard work even if you fail to achieve your goal.
All of this leads us back to the original point. We often associate positive thinking with business and entrepreneurship where it is, more often than not, a bad idea, while in education, where we have every reason to encourage positive thinking, we are constantly hearing people like Michele Rhee complain that we spend too much time building up kids' self-esteem.
Don't let the posturing and tough talk fool you. Self-esteem is good for kids and you should do everything you can to convince them that they are capable of doing every problem their teacher gives them, as long as they put in the effort.
With fantastic successes on one side and horror stories on the other, it is tempting to call this a wash, but if you think like a statistician (and you should always think like a statistician) and start breaking things down, you'll find that a few common sense rules can tell you when to assume the best and when to prepare for the worst.
Being pragmatic about being positive
For the purposes of this discussion, let's decide on a fairly precise definition of what we mean by positive thinking:
To apply positive thinking to a task, you act under the assumption that, given reasonable and intelligently applied effort, the probability of success is close to one;
Furthermore, this assumption will not be reassessed unless there is a major change in the situation.
The advantages to this approach are: we can waste a great deal of time and energy worrying; overestimating risk can cause us to prematurely abandon projects; thoughts of failure can cause us to "flinch," to hold back and not give the task our best effort. Avoiding these things can allow positive thinking to create self-fulfilling prophecies.
The disadvantages are that underestimating the probability of failure can cause us to waste resources on projects with negative expected value and, more importantly, failing to pay attention to warning signs can leave us vulnerable to otherwise avoidable disasters.
We could have a general discussion at this point about the relative weight of these advantages and disadvantages but it wouldn't be very productive because neither risk nor reward are evenly distributed. In many if not most situations, a fairly clear case can be made for either positive or cautious thinking. To determine which approach is best for a given situation, think about these rules of thumb:
Before you commit yourself, try to think realistically about the expected value in terms of other people's success rates;
Never bet more than you're willing to lose;
Consider collateral damage (are you putting your spouse and children at risk of hardship?);
Is there incremental payoff? This last one is extremely important. If you decide to start a restaurant or move to NYC to make it on Broadway, and you fail, then you will probably have very little to show for the effort. If, on the other hand, you decide to lose forty pounds through diet and exercise or to go from being a C student to an A student, then there is incremental pay off for your hard work even if you fail to achieve your goal.
All of this leads us back to the original point. We often associate positive thinking with business and entrepreneurship where it is, more often than not, a bad idea, while in education, where we have every reason to encourage positive thinking, we are constantly hearing people like Michele Rhee complain that we spend too much time building up kids' self-esteem.
Don't let the posturing and tough talk fool you. Self-esteem is good for kids and you should do everything you can to convince them that they are capable of doing every problem their teacher gives them, as long as they put in the effort.
Thursday, July 24, 2014
Recess was always my best subject
And according to this article from Tim Walker, I might have been onto something.
Like a zombie, Sami—one of my fifth graders—lumbered over to me and hissed, “I think I’m going to explode! I’m not used to this schedule.” And I believed him. An angry red rash was starting to form on his forehead.
Yikes, I thought. What a way to begin my first year of teaching in Finland. It was only the third day of school and I was already pushing a student to the breaking point. When I took him aside, I quickly discovered why he was so upset.
Throughout this first week of school, I had gotten creative with my fifth grade timetable. Normally, students and teachers in Finland take a 15-minute break after every 45 minutes of instruction. During a typical break, students head outside to play and socialize with friends while teachers disappear to the lounge to chat over coffee.
I didn’t see the point of these frequent pit stops. As a teacher in the United States, I’d spent several consecutive hours with my students in the classroom. And I was trying to replicate this model in Finland. The Finnish way seemed soft and I was convinced that kids learned better with longer stretches of instructional time. So I decided to hold my students back from their regularly scheduled break and teach two 45-minute lessons in a row, followed by a double break of 30 minutes. Now I knew why the red dots had appeared on Sami’s forehead.
Come to think of it, I wasn’t sure if the American approach had ever worked very well. My students in the States had always seemed to drag their feet after about 45 minutes in the classroom. But they’d never thought of revolting like this shrimpy Finnish fifth grader, who was digging in his heels on the third day of school. At that moment, I decided to embrace the Finnish model of taking breaks.
Once I incorporated these short recesses into our timetable, I no longer saw feet-dragging, zombie-like kids in my classroom. Throughout the school year, my Finnish students would—without fail—enter the classroom with a bounce in their steps after a 15-minute break. And most importantly, they were more focused during lessons.
At first, I was convinced that I had made a groundbreaking discovery: frequent breaks kept students fresh throughout the day. But then I remembered that Finns have known this for years; they’ve been providing breaks to their students since the 1960s.
Monday, July 21, 2014
My preferred approach to teaching high school math -- the last twenty minutes
[Dictated to my phone so beware of homonyms]
Note: Though the connection may not be immediately obvious, the following thoughts on teaching will eventually tie in with a larger piece on George Pólya.
Note: Though the connection may not be immediately obvious, the following thoughts on teaching will eventually tie in with a larger piece on George Pólya.
Though it varied someone from class to class and situation to situation, my preferred method was to reserve the last part of the class for students to work individually while I went around the room and checked each student's work. Generally, I would give the students a couple of worksheets to be handed in at the end of class. After completing those worksheets, they were instructed to spend the rest of the hour working on their homework. I wasn't always able to get to every student every day, but I came close, and I never let more than a couple of days go by without making sure that I had personally observed a student doing problems in my class.
If a lots of the students were having trouble doing the assignment, I would sometimes interrupt the routine, go back up to the board, and reteach some of the material. That was fairly rare. Most of the time, two or three students would need real help and the rest only needed either a couple of quick suggestions or simply confirmation that they were doing the problems correctly.
The personal help was important, as was the knowledge on the students' part that if they needed help in the future I would be there. This approach also let me make sure that neither the class or any of the students got into a death spiral where confusion and failure started causing a cascading effect. By personally watching students successfully completing assigned problems, I could make sure that everyone was keeping up. Grading was also an important part of that process but for assessment there is no substitute for actually watching how a kid going through a problem.
In some cases, particularly with advanced classes, I might stray from this approach, but if we are talking about at-risk kids in tough environments who need to make up ground academically, I believed then and believed now this is the best way to teach high school math.
If I sound a little over emphatic with that last sentence and perhaps even a little bitter it's because I am more than a little bitter about the direction our schools have headed. I enjoyed that kind of teaching and I got excellent results with it, but if I were to go back into the profession now, there is almost no way I could give that kind of personal attention nor could I take the same level of accountability for students' success. Class sizes have simply gotten too large.
On a completely unrelated note...
Detroit Public Schools EM shifts funds from classroom
By Dr. Thomas C. Pedroni
Many of us are shocked to learn that DPS plans to cut costs in the coming year by further increasing class sizes. Already at an unmanageable target of 38 per classroom in grades 6 through 12, Emergency Manager Jack Martin’s fiscal year 2015 budget allows class sizes in those grades to expand to 43.
Thursday, July 17, 2014
Resources for SAT self-study -- The Khan Academy
I don't want to be too negative here. This is a decent resource and for most students there will be some value in going through these problems. If that sounds like faint praise, that's because it is. What we have here, while nice, simply isn't that much to get excited about. The Academy, it should be noted, is promising a much more complete and sophisticated set of tools next year, but for now, we pretty much have to limit ourselves to the "better than nothing" standard.
I would recommend that you go to the Khan Academy SAT site and do some exploring on your own.
In the meantime, I have included a few examples to get the discussion started.
So what are my concerns here?
I The Medium is the Message
Ideally, we'd see videos that made better use of the medium (more on that later) but the bigger, more immediate concern is is that they have simply chosen the wrong message here. What we have in these two clips is basically a standard problem session with most of the good and important parts left out.
This type of instruction, done properly, is contextualized and highly interactive. Putting problems in context is essential because, even more than drudgery, the thing that drags kids down in math is not knowing why they're doing what they're doing. Working a problem for a class should be a conversation that both frames the question and gives the students a chance to participate in the solution. (For example, ask them "If this length is x, what is this other length in terms of x?" and let them come up with the 2x.) Without the conversation, there's not much point in presenting this information in a video because...
II You've already got the message in a better medium
These clips are basically an instructor reading out loud the kind of solved examples that can easily be found in books or online. The videos add little to the printed version and they arguably lose quite a bit. This will strike many as blasphemous, but for certain tasks, print actually is a superior medium. It's good at conveying precise information and it gives the reader a level of control that is difficult to achieve with pausing and rewinding a video. It offers tremendous variety and availability. It is easily searched and database-friendly. What's more, the ability to pick up a book or go to a website and teach oneself is a valuable skill for everyone and an absolutely essential ability for anyone in STEM.
Is the spoken word ever better than print? Sure, much of the time. If you're going for a conversational voice; if the gist of the message is not dependent on any single word or phrase; if you want a particular emotional tone... Unfortunately, these clips not only do things that print would do better; they leave out the things that their medium would do better than print could.
III Rush, rush, rush
There's a choppiness here both in tone and structure, combined with a hurried quality. The approach is very much "Here's a problem. Do this. Do this. Do this. Here's the answer." No time spent orienting the student. Worse yet, no time spent checking the answer. In terms of Pólya's How to Solve It, they tend to jump directly to "carrying out the plan" and stop there. That's very dangerous because, even if the students do manage to follow what you're doing, they won't have a firm grasp on why you were doing it and that's going to be a problem when you're not there to hold their hands.
IV Lots of trees, very little forest
If you want students to understand what they're doing and, just as important, if you want them not to feel confused and anxious, you have to give them a sense of the overall problem.
The carton question above is a perfect example of how to screw that up. The instructor jumps directly to the exact variables and equations needed, skipping a number of steps that are not at all obvious to the students. In fact, it is those skipped steps that trip up most of the students who miss these problems.
If you tried this with actual students, they would say "How did you know to do that?" and that's an extraordinarily good question. The answer is that we start with translation from English to mathematics (a faithful but not necessarily idiomatic translation, though I probably wouldn't mention that to the students). "[H]ow many of the $50 cartons did she buy?" suggests number of $50 cartons should be a variable (let's be original and call it x) and it makes sense that the number of $30 cartons would be another (y). "Sarah bought 20 cartons" becomes x + y = 20 and so on.
If students understand the why behind the what, they will be happier and learn better.
I don't want to be too harsh here. This isn't exactly a bad resource and I very much believe that the Khan Academy's heart is in the right place, but when it comes to the SAT, they still have a long ways to go.
Note: I made a few minor wording changes after first posting this.
I would recommend that you go to the Khan Academy SAT site and do some exploring on your own.
In the meantime, I have included a few examples to get the discussion started.
So what are my concerns here?
I The Medium is the Message
Ideally, we'd see videos that made better use of the medium (more on that later) but the bigger, more immediate concern is is that they have simply chosen the wrong message here. What we have in these two clips is basically a standard problem session with most of the good and important parts left out.
This type of instruction, done properly, is contextualized and highly interactive. Putting problems in context is essential because, even more than drudgery, the thing that drags kids down in math is not knowing why they're doing what they're doing. Working a problem for a class should be a conversation that both frames the question and gives the students a chance to participate in the solution. (For example, ask them "If this length is x, what is this other length in terms of x?" and let them come up with the 2x.) Without the conversation, there's not much point in presenting this information in a video because...
II You've already got the message in a better medium
These clips are basically an instructor reading out loud the kind of solved examples that can easily be found in books or online. The videos add little to the printed version and they arguably lose quite a bit. This will strike many as blasphemous, but for certain tasks, print actually is a superior medium. It's good at conveying precise information and it gives the reader a level of control that is difficult to achieve with pausing and rewinding a video. It offers tremendous variety and availability. It is easily searched and database-friendly. What's more, the ability to pick up a book or go to a website and teach oneself is a valuable skill for everyone and an absolutely essential ability for anyone in STEM.
Is the spoken word ever better than print? Sure, much of the time. If you're going for a conversational voice; if the gist of the message is not dependent on any single word or phrase; if you want a particular emotional tone... Unfortunately, these clips not only do things that print would do better; they leave out the things that their medium would do better than print could.
III Rush, rush, rush
There's a choppiness here both in tone and structure, combined with a hurried quality. The approach is very much "Here's a problem. Do this. Do this. Do this. Here's the answer." No time spent orienting the student. Worse yet, no time spent checking the answer. In terms of Pólya's How to Solve It, they tend to jump directly to "carrying out the plan" and stop there. That's very dangerous because, even if the students do manage to follow what you're doing, they won't have a firm grasp on why you were doing it and that's going to be a problem when you're not there to hold their hands.
IV Lots of trees, very little forest
If you want students to understand what they're doing and, just as important, if you want them not to feel confused and anxious, you have to give them a sense of the overall problem.
The carton question above is a perfect example of how to screw that up. The instructor jumps directly to the exact variables and equations needed, skipping a number of steps that are not at all obvious to the students. In fact, it is those skipped steps that trip up most of the students who miss these problems.
If you tried this with actual students, they would say "How did you know to do that?" and that's an extraordinarily good question. The answer is that we start with translation from English to mathematics (a faithful but not necessarily idiomatic translation, though I probably wouldn't mention that to the students). "[H]ow many of the $50 cartons did she buy?" suggests number of $50 cartons should be a variable (let's be original and call it x) and it makes sense that the number of $30 cartons would be another (y). "Sarah bought 20 cartons" becomes x + y = 20 and so on.
If students understand the why behind the what, they will be happier and learn better.
I don't want to be too harsh here. This isn't exactly a bad resource and I very much believe that the Khan Academy's heart is in the right place, but when it comes to the SAT, they still have a long ways to go.
Note: I made a few minor wording changes after first posting this.
Tuesday, July 15, 2014
From Scientific American -- "Don’t Take Notes with a Laptop"
Back in graduate school, I was a TA for one of the most effective college level instructors I had ever seen. She was also, perhaps not coincidentally, one of the best and most self-disciplined students I had ever seen. She was finishing her Ph.D. when I was getting my master's, so I had a chance to observe her process up close.
Her notes were particularly valued by other students. At the beginning of every semester, there would be a rush to her office to borrow the appropriate binders. The notes were compiled through a two-step process: during class she would attentively take detailed notes. She would also make audio recordings; after class she would make a second set of notes based on both her original notes and the recordings.
I was reminded of this when I came across article from SA which looks into the effectiveness of different methods of note-taking. It also raises some important questions about the role of technology in the classroom.
A Learning Secret: Don’t Take Notes with a Laptop
When it comes to college students, the belief that more is better may underlie their widely-held view that laptops in the classroom enhance their academic performance. Laptops do in fact allow students to do more, like engage in online activities and demonstrations, collaborate more easily on papers and projects, access information from the internet, and take more notes. Indeed, because students can type significantly faster than they can write, those who use laptops in the classroom tend to take more notes than those who write out their notes by hand. Moreover, when students take notes using laptops they tend to take notes verbatim, writing down every last word uttered by their professor.
Obviously it is advantageous to draft more complete notes that precisely capture the course content and allow for a verbatim review of the material at a later date. Only it isn’t. New research by Pam Mueller and Daniel Oppenheimer demonstrates that students who write out their notes on paper actually learn more. Across three experiments, Mueller and Oppenheimer had students take notes in a classroom setting and then tested students on their memory for factual detail, their conceptual understanding of the material, and their ability to synthesize and generalize the information. Half of the students were instructed to take notes with a laptop, and the other half were instructed to write the notes out by hand. As in other studies, students who used laptops took more notes. In each study, however, those who wrote out their notes by hand had a stronger conceptual understanding and were more successful in applying and integrating the material than those who used took notes with their laptops.
What drives this paradoxical finding? Mueller and Oppenheimer postulate that taking notes by hand requires different types of cognitive processing than taking notes on a laptop, and these different processes have consequences for learning. Writing by hand is slower and more cumbersome than typing, and students cannot possibly write down every word in a lecture. Instead, they listen, digest, and summarize so that they can succinctly capture the essence of the information. Thus, taking notes by hand forces the brain to engage in some heavy “mental lifting,” and these efforts foster comprehension and retention. By contrast, when typing students can easily produce a written record of the lecture without processing its meaning, as faster typing speeds allow students to transcribe a lecture word for word without devoting much thought to the content.
To evaluate this theory, Mueller and Oppenheimer assessed the content of notes taken by hand versus laptop. Their studies included hundreds of students from Princeton and UCLA, and the lecture topics ranged from bats, bread, and algorithms to faith, respiration, and economics. Content analysis of the notes consistently showed that students who used laptops had more verbatim transcription of the lecture material than those who wrote notes by hand. Moreover, high verbatim note content was associated with lower retention of the lecture material. It appears that students who use laptops can take notes in a fairly mindless, rote fashion, with little analysis or synthesis by the brain. This kind of shallow transcription fails to promote a meaningful understanding or application of the information.
...
These findings hold important implications for students who use their laptops to access lecture outlines and notes that have been posted by professors before class. Because students can use these posted materials to access lecture content with a mere click, there is no need to organize, synthesize or summarize in their own words. Indeed, students may take very minimal notes or not take notes at all, and may consequently forego the opportunity to engage in the mental work that supports learning.
Beyond altering students’ cognitive processes and thereby reducing learning, laptops pose other threats in the classroom. In the Mueller and Oppenheimer studies, all laptops were disconnected from the internet, thus eliminating any disruption from email, instant messaging, surfing, or other online distractions. In most typical college settings, however, internet access is available, and evidence suggests that when college students use laptops, they spend 40% of class time using applications unrelated to coursework, are more likely to fall off task, and are less satisfied with their education. In one study with law school students, nearly 90% of laptop users engaged in online activities unrelated to coursework for at least five minutes, and roughly 60% were distracted for half the class.
Monday, July 14, 2014
The first wall you expect is the last one you hit
[As you may have already guessed, I'm going to be tying this in with the ongoing Pólya discussion]
This is another reason why it is important for math teachers to work so hard on building your student self-confidence. Whether we are talking about calculus or golf or playing the guitar, failure usually comes when we hit one of the following walls:
Lack of ability;
Lack of time;
Lack of patience and self-discipline;
Lack of resources.
It is often the fear of these walls that prevents us from investing the time and effort into mastering a skill we would very much like to have. That is a perfectly rational attitude. As mentioned before we always judge the time and effort needed to do something against the expected returns. Unfortunately, people often have a very unrealistic concept of these returns, particularly when it comes to the placement and order of these four walls.
Students generally expect "lack of ability" to be the first wall that they hit and yet this almost never happens. After years of teaching and working with students, I honestly can't think of an example where this was the case. They run out of time; they run out of patience; they run out of resources. These are things you see all the time, but I don't know that I have ever seen a student who simply put not handle the material. I am not saying that this does not happen but I am saying that it is extremely rare.
This does not mean that the "ability wall" isn't out there somewhere. It's important to realize that even with a tremendous amount of effort and support, some goals will still be beyond you. For the extraordinarily (or perhaps more accurately, obsessively) driven, this can be a problem. I'm sure instructors at Julliard encounter this all the time. However, for those teaching math on the primary, secondary, even undergraduate level, this is probably not something you will ever have to worry about.
Kids will not be receptive to instruction, they will not respond to incentives, they will not focus on material, and they will not put forth serious effort unless you can convince them that they are not about to hit the ability wall. This may not be the most important part of mathematics instruction, but it is the first part.
This is another reason why it is important for math teachers to work so hard on building your student self-confidence. Whether we are talking about calculus or golf or playing the guitar, failure usually comes when we hit one of the following walls:
Lack of ability;
Lack of time;
Lack of patience and self-discipline;
Lack of resources.
It is often the fear of these walls that prevents us from investing the time and effort into mastering a skill we would very much like to have. That is a perfectly rational attitude. As mentioned before we always judge the time and effort needed to do something against the expected returns. Unfortunately, people often have a very unrealistic concept of these returns, particularly when it comes to the placement and order of these four walls.
Students generally expect "lack of ability" to be the first wall that they hit and yet this almost never happens. After years of teaching and working with students, I honestly can't think of an example where this was the case. They run out of time; they run out of patience; they run out of resources. These are things you see all the time, but I don't know that I have ever seen a student who simply put not handle the material. I am not saying that this does not happen but I am saying that it is extremely rare.
This does not mean that the "ability wall" isn't out there somewhere. It's important to realize that even with a tremendous amount of effort and support, some goals will still be beyond you. For the extraordinarily (or perhaps more accurately, obsessively) driven, this can be a problem. I'm sure instructors at Julliard encounter this all the time. However, for those teaching math on the primary, secondary, even undergraduate level, this is probably not something you will ever have to worry about.
Kids will not be receptive to instruction, they will not respond to incentives, they will not focus on material, and they will not put forth serious effort unless you can convince them that they are not about to hit the ability wall. This may not be the most important part of mathematics instruction, but it is the first part.
Friday, July 11, 2014
Rational students, incentives and expected returns
In my last post, I contrasted George Pólya's humanistic style of teaching with the scientific management approach favored by most movement reformers. The focus of that post was more on the underlying philosophy (I'd contend that George Pólya had a very different view of people than did Frederick Taylor), but there are some extremely practical reasons for adopting Pólya's approach, particularly when it comes to building students' self-confidence.
Every investment involves a comparison of costs vs. expected value. We never know how a decision will turn out, so we have to balance money, time and trouble against expected returns. I realize this point seems to border on too-obvious-to-mention but it's surprising how often people forget there are random variables in their arguments, sometimes with disastrous results.
Take performance-based incentives. Let's say I'm going to offer to pay you a certain sum if you accomplish a task but nothing if you fail. In order for you to agree, your time and effort will have to be valued less than the product of my offer times the likelihood of success. Once again at the risk of stating the obvious, as that likelihood approaches zero, your idea of a reasonable offer will have to approach infinity. Of course, in real life, there are always bounds on the amount of money I can offer but your estimate of the likelihood of success can always get closer to zero.
In a business context, we normally deal with the small perceived likelihood problem by finding someone else or opting for a different compensation plan or simply walking away from the deal. This is yet another reason why it's dangerous to have people who don't thoroughly understand both business and education try to transplant ideas from one field to another (it also reminds us of Pólyas warning that "it is foolish to answer a question you do not understand").
In education, where we should try to reach every student, low perceived likelihoods of success can be deadly. Any reward you offer for an apparently unattainable success will seem worthless; any penalty for apparently inevitable failure will seem brutally unfair. If you want to motivate these students, you will have to convince them that, with reasonable time and effort, the odds of success are pretty good (this happens to be true for the vast majority of students but that's a topic for another post).
Pólya said "If the student is not able to do much, the teacher should leave him at least some illusion of independent work." This was, of course, meant as a last resort, but his point was that students absolutely have to think of math as something they are capable of doing.
Every investment involves a comparison of costs vs. expected value. We never know how a decision will turn out, so we have to balance money, time and trouble against expected returns. I realize this point seems to border on too-obvious-to-mention but it's surprising how often people forget there are random variables in their arguments, sometimes with disastrous results.
Take performance-based incentives. Let's say I'm going to offer to pay you a certain sum if you accomplish a task but nothing if you fail. In order for you to agree, your time and effort will have to be valued less than the product of my offer times the likelihood of success. Once again at the risk of stating the obvious, as that likelihood approaches zero, your idea of a reasonable offer will have to approach infinity. Of course, in real life, there are always bounds on the amount of money I can offer but your estimate of the likelihood of success can always get closer to zero.
In a business context, we normally deal with the small perceived likelihood problem by finding someone else or opting for a different compensation plan or simply walking away from the deal. This is yet another reason why it's dangerous to have people who don't thoroughly understand both business and education try to transplant ideas from one field to another (it also reminds us of Pólyas warning that "it is foolish to answer a question you do not understand").
In education, where we should try to reach every student, low perceived likelihoods of success can be deadly. Any reward you offer for an apparently unattainable success will seem worthless; any penalty for apparently inevitable failure will seem brutally unfair. If you want to motivate these students, you will have to convince them that, with reasonable time and effort, the odds of success are pretty good (this happens to be true for the vast majority of students but that's a topic for another post).
Pólya said "If the student is not able to do much, the teacher should leave him at least some illusion of independent work." This was, of course, meant as a last resort, but his point was that students absolutely have to think of math as something they are capable of doing.
Wednesday, July 9, 2014
Pólya was a humanist. That puts him at odds with the education reform movement.
What do I mean when I say that George Pólya was a humanist and imply that movement reformers (at least the ones that matter) are not? All too often, people use 'humanist' or 'humanistic' simply as an impressive way of saying nice or decent. While I certainly believe that Pólya was both a nice and decent man, I have something much more specific in mind here.
Pólya's approach to mathematics pedagogy was humanistic in the sense that it was based on certain assumptions about human nature, viewing students as playful and inquisitive animals who were naturally inclined to learn and to solve problems. That natural inclination meant that the best way to help students was through "common sense" suggestions (a phrase that featured prominently in How To Solve It).
He also focused a great deal of attention on the emotional and psychological state of the student. It was explicitly part of the teacher's job to instill self esteem, self-confidence, and self-reliance in the student, even if it occasionally meant giving the student an exaggerated sense of accomplishment.
"If the student is not able to do much, the teacher should leave him at least some illusion of independent work. In order to do so, the teacher should help the student discreetly, unobtrusively." [emphasis in the original text.]
This humanistic view of learning math lead unsurprisingly to a similar view of teaching with a strong emphasis on empathy and individuality:
"The teacher should put himself in the student's place, he should see the student's case, he should try to understand what is going on in the student's mind and ask a question or indicate a step that could have occurred to the student himself." [emphasis in the original text.]
In order to see how this figures in the larger education debate, we need to introduce the field of scientific management. This field is largely based on the idea that people can be treated like any other component in a complex system. The secret to optimal performance is simply to gather the right data, derive the proper metrics, then use these metrics to put the right components in the right roles and create optimal set of incentives.
The education reform movement with its emphasis on metrics, standardization, and scripted lessons is entirely derived from scientific management. Those scripted lessons in particular represent a complete rejection of Pólya's approach of "getting inside the students head." and personalizing the instruction. Not coincidentally, David Coleman, arguably the intellectual leader of the movement, started out as a management consultant.
Another area of sharp contrast between David Coleman and Pólya is Coleman's strong support of deliberate practice in mathematics education. Scientific management is heavily reliant on reductionist approaches and their are few pedagogical techniques more reductionist than deliberate practice. Pólya was wary of reductionist approaches to teaching. He saw drills as a sometimes necessary evil, but as a rule, breaking down problems for the student was a dangerous habit. For Pólya, the process of problem solving was about taking problems and examining them, restating them, generalizing them, simplifying them, comparing them to other problems, and, yes, breaking them down into sub-problems, but the important part of that process is deciding what to do. To break the problem down for the student is to defeat the purpose.
Many, if not most, of those horrible, multi-step math problems which have become associated with Common Core are not what Pólya would consider problems at all. The problem solving has all been done in the preparation of the lesson; all that's left for the student is the mechanics.
As a side note, Pólya believed that any method you use to solve a problem was acceptable as long as you understood the problem and could prove that your answer was right. This included guessing. Pólya even joked that his initials stood for "Guess and Prove." This approach allowed him to make a string of major discoveries in Twentieth Century mathematics but it would not have gotten him a passing grade in a Coomon Core influenced elementary school.
Pólya's humanistic approach no doubt reflected and underlying philosophy but there was another more practical reason for adopting this approach. Put bluntly, after a long and successful career doing and teaching mathematics, Pólya had a strong sense of what worked. I will get into the practical underpinnings of Pólya's humanism in the next post.
Pólya's approach to mathematics pedagogy was humanistic in the sense that it was based on certain assumptions about human nature, viewing students as playful and inquisitive animals who were naturally inclined to learn and to solve problems. That natural inclination meant that the best way to help students was through "common sense" suggestions (a phrase that featured prominently in How To Solve It).
He also focused a great deal of attention on the emotional and psychological state of the student. It was explicitly part of the teacher's job to instill self esteem, self-confidence, and self-reliance in the student, even if it occasionally meant giving the student an exaggerated sense of accomplishment.
"If the student is not able to do much, the teacher should leave him at least some illusion of independent work. In order to do so, the teacher should help the student discreetly, unobtrusively." [emphasis in the original text.]
This humanistic view of learning math lead unsurprisingly to a similar view of teaching with a strong emphasis on empathy and individuality:
"The teacher should put himself in the student's place, he should see the student's case, he should try to understand what is going on in the student's mind and ask a question or indicate a step that could have occurred to the student himself." [emphasis in the original text.]
In order to see how this figures in the larger education debate, we need to introduce the field of scientific management. This field is largely based on the idea that people can be treated like any other component in a complex system. The secret to optimal performance is simply to gather the right data, derive the proper metrics, then use these metrics to put the right components in the right roles and create optimal set of incentives.
The education reform movement with its emphasis on metrics, standardization, and scripted lessons is entirely derived from scientific management. Those scripted lessons in particular represent a complete rejection of Pólya's approach of "getting inside the students head." and personalizing the instruction. Not coincidentally, David Coleman, arguably the intellectual leader of the movement, started out as a management consultant.
Another area of sharp contrast between David Coleman and Pólya is Coleman's strong support of deliberate practice in mathematics education. Scientific management is heavily reliant on reductionist approaches and their are few pedagogical techniques more reductionist than deliberate practice. Pólya was wary of reductionist approaches to teaching. He saw drills as a sometimes necessary evil, but as a rule, breaking down problems for the student was a dangerous habit. For Pólya, the process of problem solving was about taking problems and examining them, restating them, generalizing them, simplifying them, comparing them to other problems, and, yes, breaking them down into sub-problems, but the important part of that process is deciding what to do. To break the problem down for the student is to defeat the purpose.
Many, if not most, of those horrible, multi-step math problems which have become associated with Common Core are not what Pólya would consider problems at all. The problem solving has all been done in the preparation of the lesson; all that's left for the student is the mechanics.
As a side note, Pólya believed that any method you use to solve a problem was acceptable as long as you understood the problem and could prove that your answer was right. This included guessing. Pólya even joked that his initials stood for "Guess and Prove." This approach allowed him to make a string of major discoveries in Twentieth Century mathematics but it would not have gotten him a passing grade in a Coomon Core influenced elementary school.
Pólya's humanistic approach no doubt reflected and underlying philosophy but there was another more practical reason for adopting this approach. Put bluntly, after a long and successful career doing and teaching mathematics, Pólya had a strong sense of what worked. I will get into the practical underpinnings of Pólya's humanism in the next post.
Monday, April 28, 2014
SAT tips -- the opposite of the worst test you ever took
[This is part of an ongoing series of posts designed to help students, parents, teachers and other interested bystanders learn about and prepare for the SAT]
A message for perspective test takers...
No, really. Think back over the tests you've taken over all the years. Now think about the ones that caught you completely off guard. The ones that covered material you hadn't expected, asked questions completely different than what you expected. If you've ever had a test like that you probably still remember that feeling of being surprised, unprepared, even lied to, and worst of all, helpless.
If you're like me, those were probably the worst test-taking experiences you've ever had.
What would the opposite of a test like that be? What about one where the teacher gave you a stack of all of the old tests over that section going back ten years? On top of that, what if the teacher promised to keep the test as similar as possible to all those old tests, same material covered, same format, same type of questions, same difficulty? Wouldn't that pretty much be the opposite?
That's what we have with the SAT. The company that makes the test has been releasing its old tests for decades. You can buy collections of old tests in almost any book store. Better yet, you can get them for free from your school library.
And you usually don't have to worry about the new tests throwing in a lot of big changes. This next year might be an exception (there's been lots of talk about 'reforming' the test), but in general the SAT changes very slowly. This next year might be the exception, but other than that if you get a collection of old tests and work through them, asking your teachers for help whenever you get confused, you'll find that the SAT is exactly the test you expected and prepared for.
And that's a very good feeling.
A message for perspective test takers...
No, really. Think back over the tests you've taken over all the years. Now think about the ones that caught you completely off guard. The ones that covered material you hadn't expected, asked questions completely different than what you expected. If you've ever had a test like that you probably still remember that feeling of being surprised, unprepared, even lied to, and worst of all, helpless.
If you're like me, those were probably the worst test-taking experiences you've ever had.
What would the opposite of a test like that be? What about one where the teacher gave you a stack of all of the old tests over that section going back ten years? On top of that, what if the teacher promised to keep the test as similar as possible to all those old tests, same material covered, same format, same type of questions, same difficulty? Wouldn't that pretty much be the opposite?
That's what we have with the SAT. The company that makes the test has been releasing its old tests for decades. You can buy collections of old tests in almost any book store. Better yet, you can get them for free from your school library.
And you usually don't have to worry about the new tests throwing in a lot of big changes. This next year might be an exception (there's been lots of talk about 'reforming' the test), but in general the SAT changes very slowly. This next year might be the exception, but other than that if you get a collection of old tests and work through them, asking your teachers for help whenever you get confused, you'll find that the SAT is exactly the test you expected and prepared for.
And that's a very good feeling.
Friday, April 25, 2014
The SAT and the penalty for NOT guessing
[I'm about to start a major SAT thread, so I thought I'd lay some groundwork by reposting something I wrote a few weeks ago on the analytics blog West Coast Stat Views. I'll be elaborating more on the widely misunderstood correction for guessing in future You Do the Math posts.]
Last week we had a post on why David Coleman's announcement that the SAT would now feature more "real world" problems was bad news, probably leading to worse questions and almost certainly hurting the test's orthogonality with respect to GPA and other transcript-based variables. Now let's take a at the elimination of the so-called penalty for guessing.
The SAT never had a penalty for guessing, not in the sense that guessing lowed your expected score. What the SAT did have was a correction for guessing. On a multiple-choice test without the correction (which is to say, pretty much all tests except the SAT), blindly guessing on the questions you didn't get a chance to look at will tend to raise your score. Let's say, for example, two students took a five-option test where they knew the answers to the first fifty questions and had no clue what the second fifty were asking (assume they were in Sanskrit). If Student 1 left the Sanskrit questions blank, he or she would get fifty point on the test. If Student 2 answered 'B' to all the Sanskrit questions, he or she would probably get around sixty points.
From an analytic standpoint, that's a big concern. We want to rank the students based on their knowledge of the material but here we have two students with the same mastery of the material but with a ten-point difference in scores. Worse yet, let's say we have a third student who knows a bit of Sanskrit and manages to answer five of those questions, leaving the rest blank thus making fifty-five points. Student 3 knows the material better than Student 2 but Student 2 makes a higher score. That's pretty much the worst possible case scenario for a test.
Now let's say that we subtracted a fraction of a point for each wrong answer -- 1/4 in this case, 1/(number of options - 1) in general -- but not for a blank. Now Student 1 and Student 2 both have fifty points while Student 3 still has fifty-five. The lark's on the wing, the snail's on the thorn, the statistician has rank/ordered the population and all's right with the world.
[Note that these scales are set to balance out for blind guessing. Students making informed guesses ("I know it can't be 'E'") will still come out ahead of those leaving a question blank. This too is as it should be.]
You can't really say that Student 2 has been penalized for guessing since the outcome for guessing is, on average, the same as the outcome for not guessing. It would be more accurate to say that 1 and 3 were originally penalized for NOT guessing.
Compared to some of the other issues we've discussed regarding the SAT, this one is fairly small, but it does illustrate a couple of important points about the test. First, the SAT is a carefully designed tests and second, some of the recent changes aren't nearly so well thought out.
Last week we had a post on why David Coleman's announcement that the SAT would now feature more "real world" problems was bad news, probably leading to worse questions and almost certainly hurting the test's orthogonality with respect to GPA and other transcript-based variables. Now let's take a at the elimination of the so-called penalty for guessing.
The SAT never had a penalty for guessing, not in the sense that guessing lowed your expected score. What the SAT did have was a correction for guessing. On a multiple-choice test without the correction (which is to say, pretty much all tests except the SAT), blindly guessing on the questions you didn't get a chance to look at will tend to raise your score. Let's say, for example, two students took a five-option test where they knew the answers to the first fifty questions and had no clue what the second fifty were asking (assume they were in Sanskrit). If Student 1 left the Sanskrit questions blank, he or she would get fifty point on the test. If Student 2 answered 'B' to all the Sanskrit questions, he or she would probably get around sixty points.
From an analytic standpoint, that's a big concern. We want to rank the students based on their knowledge of the material but here we have two students with the same mastery of the material but with a ten-point difference in scores. Worse yet, let's say we have a third student who knows a bit of Sanskrit and manages to answer five of those questions, leaving the rest blank thus making fifty-five points. Student 3 knows the material better than Student 2 but Student 2 makes a higher score. That's pretty much the worst possible case scenario for a test.
Now let's say that we subtracted a fraction of a point for each wrong answer -- 1/4 in this case, 1/(number of options - 1) in general -- but not for a blank. Now Student 1 and Student 2 both have fifty points while Student 3 still has fifty-five. The lark's on the wing, the snail's on the thorn, the statistician has rank/ordered the population and all's right with the world.
[Note that these scales are set to balance out for blind guessing. Students making informed guesses ("I know it can't be 'E'") will still come out ahead of those leaving a question blank. This too is as it should be.]
You can't really say that Student 2 has been penalized for guessing since the outcome for guessing is, on average, the same as the outcome for not guessing. It would be more accurate to say that 1 and 3 were originally penalized for NOT guessing.
Compared to some of the other issues we've discussed regarding the SAT, this one is fairly small, but it does illustrate a couple of important points about the test. First, the SAT is a carefully designed tests and second, some of the recent changes aren't nearly so well thought out.
Wednesday, March 5, 2014
A challenging standardized test geometry problem
[If you thought the last two problems in the series were too easy, this might be more your speed.]
Circle 1 and Circle 2 both have radius 2. Each passes through the center of the other. Find the area of the rhombus formed by the two points of intersection (A and B) and the centers of each circle (C1 and C2).
Circle 1 and Circle 2 both have radius 2. Each passes through the center of the other. Find the area of the rhombus formed by the two points of intersection (A and B) and the centers of each circle (C1 and C2).
Saturday, January 11, 2014
"An engineer,,, can hire a mathematician to solve his mathematical problems for him" -- Pólya on word problems
George Pólya writing in the book Mathematical Discovery:
I hope that I shall shock a few people in asserting that the most important single task of mathematical instruction in the secondary schools is to teach the setting up of equations to solve word problems. Yet there is a strong argument in favor of this opinion.
In solving a word problem by setting up equations, the student translates a real situation into mathematical terms: he has an opportunity to experience that mathematical concepts may be related to realities, but such relations must be carefully worked out. Here is the first opportunity afforded by the curriculum for this basic experience. This first opportunity may be also the last for a student who will not use mathematics in his profession. Yet engineers and scientists who will use mathematics professionally, will use it mainly to translate real situations into mathematical concepts. In fact, an engineer makes more money than a mathematician and so he can hire a mathematician to solve his mathematical problems for him; therefore, the future engineer need not study mathematics to solve problems. Yet, there is one task for which the engineer cannot fully rely on the mathematician: the engineer must know enough mathematics to set up his problems in mathematical form. And so the future engineer, when he learns in the secondary school to set up equations to solve “word problems,” has a first taste of, and has an opportunity to acquire the attitude essential to, his principal professional use of mathematics.
Subscribe to:
Comments (Atom)










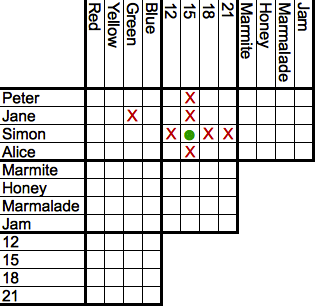







%2B059CLEANbrightdim660x900comp92.jpg)







