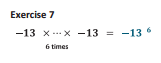We may differ on the definition of "has been corrected"

As part of a response the the recent piece in the Washington Post, Jill Diniz (Director of Eureka Math/Great Minds) said [emphasis added]:

The missing parentheses noted by the blogger, when introducing the concept of raising a negative number to a positive integer, was caused by converting the online curriculum to PDFs. This has been corrected. A benefit of open educational resources, such as Eureka Math, is they are easier than traditional instructional resources to improve upon quickly. 

Putting aside the concerns this raises about editing, proofing and overall quality control, let's take a minute and check the corrected version.

In case the print is too small, here are a couple of crops:

MOO?s

[I'm in full mad-scientist mode here, so things may be a bit incoherent in places but I do have some more realistic (or at least, less febrile) plans in the queue.]

MOOC advocates like Friedman have been both wildly ambitious about the potential impact of the technology and strangely timid about pushing its boundaries. Mostly, they fall back on the catalytic theory of educational technology. Rather than doing hard thinking about what different media are good at, they simply assume that the presence of technology will automatically make things better.

For all the talk about reinventing the form, MOOCS still tend to look pretty much like this:

A series of lessons and assignments given in a specific order, in other words, just like any other course..

Why are courses so linear? Because the current system is based on having instructors interact face-to-face with large numbers of students, and the only cost-efficient way to do this on a large scale is to collect the students in groups and take them through standardized instruction. We can go back-and-forth on the value of this face-to-face interaction, but it is clear that, once you have eliminated this requirement, you have no need for this level of standardization.

Even if we accept the necessity of having everybody take a common set of exams (and I am not entirely prepared to concede that one either), there is still no reason for all students in a MOOC to take the same instructional units in the same order.

Instead of thinking lesson one, lesson two, exam one, lesson three, exam two and so forth ad nauseam, we should probably be thinking more in the lines of this:

We have some kind of assessment. Based on the results of that assessment, the student is sent to a certain module. That module could be pretty much anything. The student could be directed to watch a video clip, listen to an audio file, read a section of text, play a game, chat with an instructor, or even have a tutoring session or study group. Even the assessments might vary based on path.

In addition to being customized to each student and allowing for an wide array of modules, the MOO? is an evolving format. Assessments can be changed, paths can shift, and, most importantly, more modules can always be added (possibly even user based content).

I know this is all very rough and inchoate, but I do plan to get specific in the near future, starting with our old friend, Eugen Weber.

From the ashes of New Math

One of my big concerns with the education reform debate, particularly as it regards mathematics, is that a great deal of the debate consist of words being thrown around that have a positive emotional connotation, but which are either vague or worse yet mean different things to different participants in the discussion.

As a result, you have a large number of "supporters" of common core who are, in fact, promoting entirely different agendas and probably not realizing it (you might be able to say the same about common core opponents but, by nature, opposition is better able to handle a lack of coherence) . I strongly suspect this is one of the causes behind the many problems we've seen in Eureka math and related programs. The various contributors were working from different and incompatible blueprints.

There's been a great deal of talk about improving mathematics education, raising standards, teaching problem-solving, and being more rigorous. All of this certainly sounds wonderful, but it is also undeniably vague. When you drill down, you learn that different supporters are using the same words in radically different senses .

For David Coleman and most of the non-content specialists, these words mean that all kids graduating high school should be college and career-ready, especially when it comes to the STEM fields which are seen as being essential to future economic growth.

(We should probably stop here and make a distinction between STEM and STEAM – science technology engineering applied mathematics. Coleman and Company are definitely talking about steam)

Professor Wu (and I suspect many of the other mathematicians who have joined into the initiative) is defining rigor much more rigorously. For him, the objective is to teach mathematics in a pure form, an axiomatic system where theorems build upon theorems using rules of formal logic. This is not the kind of math class that most engineers advocate; rather it is the kind of math class that most engineers complain about. (Professor Wu is definitely not a STEAM guy.)

In the following list taken from this essay from Professor Wu, you can get a feel for just how different his philosophy is from David Coleman's. The real tip-off is part 3. The suggestion that every formula or algorithm be logically derived before it can be used has huge implications, particularly as we move into more applied topics. (Who here remembers calculus? Okay, and who here remembers how to prove the fundamental theorem of calculus?)

All of Professor Wu's arguments are familiar to anyone who has studied the history of New Math in the 60s. There is no noticeable daylight between the two approaches.

I don't necessarily mean this as a pejorative. Lots of smart people thought that new math was a good idea in the late 50s and early 60s; I'm sure that quite a few smart people still think so today. I personally think it's a very bad idea but that's a topic for another post. For now though, the more immediate priority is just understand exactly what we're arguing about.

The Fundamental Principles of Mathematics

I believe there are five interrelated, fundamental principles of mathematics.
They are routinely violated in school textbooks and in the math education
literature, so teachers have to be aware of them to teach well.

1. Every concept is precisely defined, and definitions furnish the basis for logical
deductions. At the moment, the neglect of definitions in school mathematics has reached the point at which many teachers no longer know the difference between a definition and a theorem. The general perception among the hundreds of teachers I have worked with is that a definition is “one more thing to memorize.” Many bread-and-butter concepts of K–12 mathematics are not correctly defined or, if defined, are not put to use as integral parts of reasoning. These include number, rational number (in middle school), decimal (as a fraction in upper elementary school), ordering of fractions, product of fractions, division of fractions, length-area-volume (for different grade levels), slope of a line, half-plane of a line, equation, graph of an equation, inequality between functions, rational exponents of a positive number, polygon, congruence, similarity, parabola, inverse function, and polynomial.

2. Mathematical statements are precise. At any moment, it is clear what is known and what is not known. There are too many places in school mathematics in which textbooks and other education materials fudge the boundary between what is true and what is not. Often a heuristic argument is conflated with correct logical reasoning. For example, the identity √a√b = √ab for positive numbers a and b is often explained by assigning a few specific values to a and b and then checking for these values with a calculator. Such an approach is a poor substitute for mathematics because it leaves open the possibility that there are other values for a and b for which the identity is not true.

3. Every assertion can be backed by logical reasoning. Reasoning is the lifeblood of mathematics and the platform that launches problem solving. For example, the rules of place value are logical consequences of the way we choose to count. By choosing to use 10 symbols (i.e., 0 to 9), we are forced to use no more than one position (place) to be able to count to large numbers. Given the too frequent absence of reasoning in school mathematics, how can we ask students to solve problems if teachers have not been prepared to engage students in logical reasoning on a consistent basis?

4. Mathematics is coherent; it is a tapestry in which all the concepts and skills are logically interwoven to form a single piece. The professional development of math teachers usually emphasizes either procedures (in days of yore) or intuition (in modern times), but not the coherent structure of mathematics. This may be the one aspect of mathematics that most teachers (and, dare I say, also math education professors) find most elusive. For instance, the lack of awareness of the coherence of the number systems in K–12 (whole numbers, integers, fractions, rational numbers, real numbers, and complex numbers) may account for teaching fractions as “different from” whole numbers such that the learning of fractions becomes almost divorced from the learning of whole numbers. Likewise, the resistance that some math educators (and therefore teachers) have to explicitly teaching children the standard algorithms may arise from not knowing the coherent structure that underlies these algorithms: the essence of all four standard algorithms is the reduction of any whole number computation to the computation of single-digit numbers.

5. Mathematics is goal oriented, and every concept or skill has a purpose. Teachers who recognize the purposefulness of mathematics gain an extra tool to make their lessons more compelling. For example, when students see the technique of completing the square merely as a trick to get the quadratic formula, rather than as the central idea underlying the study of quadratic functions, their understanding of the technique is superficial. Mathematics is a collection of interconnecting chains in which each concept or skill appears as a link in a chain, so that each concept or skill serves the purpose of supporting another one down the line. Students should get to see for themselves that the mathematics curriculum moves forward with a purpose.

At the risk of putting too fine of a point on it, this approach tends to produce extremely formal and dense prose such the following (from a company Professor Wu was involved with):

Dilation: A transformation of the plane with center O and scale factor r(r > 0). If
D(O) = O and if P ≠ O, then the point D(P), to be denoted by Q, is the point on the ray OP so that |OQ| = r|OP|. If the scale factor r ≠ 1, then a dilation in the coordinate plane is a transformation that shrinks or magnifies a figure by multiplying each coordinate of the figure by the scale factor.

Congruence: A finite composition of basic rigid motions—reflections, rotations,
translations—of the plane. Two figures in a plane are congruent if there is a congruence that maps one figure onto the other figure.

Similar: Two figures in the plane are similar if a similarity transformation exists, taking one figure to the other.

Similarity Transformation: A similarity transformation, or similarity, is a composition of a finite number of basic rigid motions or dilations. The scale factor of a similarity transformation is the product of the scale factors of the dilations in the composition; if there are no dilations in the composition, the scale factor is defined to be 1.

Similarity: A similarity is an example of a transformation.

Opposite day at the Common Core debate

I recently came across this defense of Common Core by two Berkeley mathematicians, Edward Frenkel and Hung-Hsi Wu. Both are sharp and highly respected and when you hear about serious mathematicians supporting the initiative, there's a good chance these two names will be on the list that follows.

Except they don't support it. They support something they call Common Core, but what they describe is radically different than what the people behind the program are talking about. The disconnect is truly amazing. Wu and Frenkel's description of common core doesn't just disagree with that used by David Coleman and pretty much everyone else involved with the enterprise; it openly contradicts it.

The case that Coleman made to Bill Gates and stuck with since then is that "academic standards varied so wildly between states that high school diplomas had lost all meaning". Furthermore, Coleman argued that having a uniform set of national standards would allow us to use a powerful set of administrative tools. We could create metrics, track progress, set up incentive systems, and generally tackle the problem like management consultants.

Compare that to this excerpt from Wu and Frenkel's essay [emphasis added]:

Before the CCSSM were adopted, we already had a de facto national curriculum in math because the same collection of textbooks was (and still is) widely used across the country. The deficiencies of this de facto national curriculum of "Textbook School Mathematics" are staggering. The CCSSM were developed precisely to eliminate those deficiencies, but for CCSSM to come to life we must have new textbooks written in accordance with CCSSM. So far, this has not happened and, unfortunately, the system is set up in such a way that the private companies writing textbooks have more incentive to preserve the existing status quo maximizing their market share than to get their math right. The big elephant in the room is that as of today, less than a year before the CCSSM are to be fully implemented, we still have no viable textbooks to use for teaching mathematics according to CCSSM!

The situation is further aggravated by the rush to implement CCSSM in student assessment. A case in point is the recent fiasco in New York State, which does not yet have a solid program for teaching CCSSM, but decided to test students according to CCSSM anyway. The result: students failed miserably. One of the teachers wrote to us about her regrets that "the kids were not taught Common Core" and that it was "tragic" how low their scores were. How could it be otherwise? Why are we testing students on material they haven't been taught? Of course, it is much easier and more fun, in lieu of writing good CCSSM textbooks, to make up CCSSM tests and then pat each other on the back and wave a big banner: "We have implemented Common Core -- Mission accomplished." But no one benefits from this. Are we competing to create a Potemkin village, or do we actually care about the welfare of the next generation? What happened in New York State will happen next year across the country if we don't get our act together.

[As a side remark, we note that even in the best of circumstances, it's a big question how to effectively test students in math on a large scale. Developing such tests is an art form still waiting to be perfected, and in any case, it's not clear how accurately students' scores on these tests can reflect students' learning. Unfortunately, our national obsession with the test scores has forced teachers to teach to the test rather than teach the material for learning. While we consider some form of standardized assessment to be necessary (just as driver's license tests are necessary), we deplore this obsession. It is time to put the emphasis back on student learning inside the classroom.]

These misguided practices give a bad name to CCSSM, which is being exploited by the standards' opponents. They misinform the public by equating CCSSM with ill-fated assessments, such as the one in New York State, when in fact the problem is caused mostly by the disconnect between the current Textbook School Mathematics and CCSSM. It is for this reason that having the CCSSM is crucial, because this is what will ensure that students are taught correct mathematics rather than the deficient and obsolete Textbook School Mathematics.

It is possible and necessary to create mathematics textbooks that do better than Textbook School Mathematics. One such effort by commoncore.org holds promise: its Eureka Math series will make online courses in K-12 math available at a modest cost. The series will be completed sometime in 2014. [Full disclosure: one of us is an author of the 8th grade textbook in that series.]

The authors have contradicted both major components of Coleman's argument. They insist that we already have a relatively consistent national system of mathematics standards and furthermore they question the reliability of the metrics which Coleman's entire system is based upon.

How can proponents of common core hold such mutually exclusive use and yet be largely unaware of the contradictions?

I suspect it is some combination of poor communication and wishful thinking on both sides. As spelled out in this essay by Wu, the authors desperately want to see mathematics education returned to some kind of Euclidean ideal. A rigorous axiomatic approach where all lessons start with precise definitions and proceed through a series of logical deductions. They have convinced themselves that the rest of the Common Core establishment is in sympathy with them just as they have convinced themselves that the lessons being produced by Eureka math are rigorous and accurate.

Well, it's funny to math majors

A few years ago, when I was teaching math at a big state university, a colleague told me the following.

She was comparing notes with a professor at a nearby school on how their respective real analysis courses were going. She told him that they had just proved that the square root of two was an irrational number. He laughed and said she was way ahead of him; his class had just proved that the square root of two is a number.

[Don't feel bad if you don't get it. This is not the sort of thing that normal people talk about.]

The joke was that, while it may sound impressive, showing that the square root of two is irrational is fairly easy. There's a nice, elegant little proof that is easy to explain and is suitable for anyone who has completed the first few sections of high school algebra. On the other hand, showing that a real number X exist such that X squared equals two is actually a bit of a challenge.

There is one other point here which ties in to our ongoing math curriculum thread. Namely that, with the borderline exception of high school geometry (and even there we cheat a little), a truly rigorous approach to lower level mathematics is wildly impractical. The order in which concepts are needed does not match up at all with the order of difficulty of proof (the fundamental theorem of calculus comes to mind). Therefore much (probably most) of what we tell students is back up with no more than a "trust us." We don't have to like this but we do have to acknowledge it.

This doesn't mean that proofs aren't important, but that the importance lies in the process and not in the result.